Дифференцирующие и интегрирующие RC-цепи.

Обсудив в предыдущих статьях устройство и принцип работы резисторов, конденсаторов и катушек индуктивности, мы имеем полное право перейти к рассмотрению цепей, состоящих из этих элементов 🙂 Этим мы сегодня и займемся.

И первая цепь, работу которой мы рассмотрим – дифференцирующая RC-цепь.

Дифференцирующая RC-цепь.

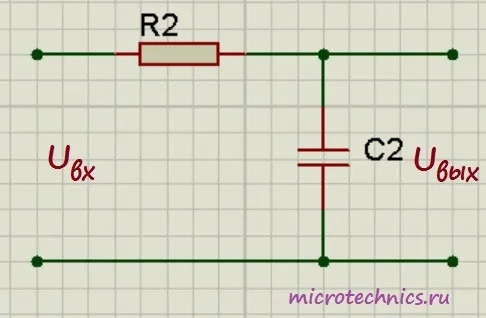
Из названия цепи, в принципе, уже понятно, что за элементы входят в ее состав – это конденсатор и резистор 🙂 И выглядит она следующим образом:

Работа данной схемы основана на том, что ток, протекающий через конденсатор, прямо пропорционален скорости изменения напряжения, приложенного к нему:

$i = C \frac{dU_c}{dt}$

Напряжения в цепи связаны следующим образом (по закону Кирхгофа):

$u_{out} = u_{in} - u_c$

В то же время, по закону Ома мы можем записать:

$u_{out} = i R = C R \frac{dU_c}{dt}$

Выразим $u_C$ из первого выражения и подставим во второе:

$u_{out} = C R \frac{dU_c}{dt} = C R (\frac{dU_{in}}{dt} - \frac{dU_{out}}{dt})$

$u_{out} = C R \frac{dU_{in}}{dt} - C R \frac{dU_{out}}{dt}$

При условии, что $C R \frac{dU_{out}}{dt} << u_{out}$ (то есть скорость изменения напряжения низкая) мы получаем приближенную зависимость для напряжения на выходе:

$u_{out} \approx C R \frac{dU_{in}}{dt}$

Таким образом, цепь полностью оправдывает свое название, ведь напряжение на выходе представляет из себя дифференциал входного сигнала.

Но возможен еще и другой случай, когда $C R \frac{dU_{out}}{dt} >> u_{out}$ (быстрое изменение напряжения). При выполнении этого равенства мы получаем такую ситуацию:

$C R \frac{dU_{in}}{dt} = C R \frac{dU_{out}}{dt}$

То есть: $U_{out} \approx U_{in}$ .

Можно заметить, что условие $C R \frac{dU_{out}}{dt} << u_{out}$ будет лучше выполняться при небольших значениях произведения $C R$ , которое называют постоянной времени цепи:

$\tau = R C$

Давайте разберемся, какой смысл несет в себе эта характеристика цепи 🙂

Заряд и разряд конденсатора происходит по экспоненциальному закону:

$u = U_0 e^{-\frac{t}{\tau}}$

Здесь $U_0$ – напряжение на заряженном конденсаторе в начальный момент времени. Давайте посмотрим, каким будет значение напряжения по истечении времени $\tau$ :

$U_{\tau} = U_0 e^{-\frac{\tau}{\tau}} = U_0 e^{-1} \approx 0.37 U_0$

Напряжение на конденсаторе уменьшится до 37% от первоначального.

Получается, что $\tau$ – это время, за которое конденсатор:

при заряде – зарядится до 63%
при разряде – разрядится на 63% (разрядится до 37%)

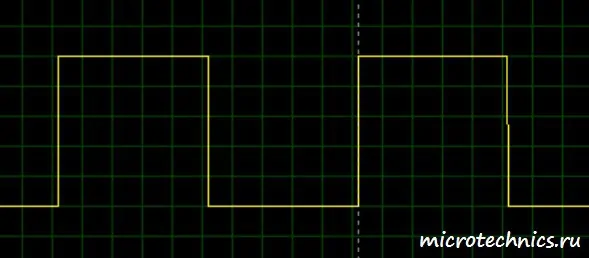
С постоянной времени цепи мы разобрались, давайте вернемся к дифференцирующей RC-цепи 🙂

Теоретические аспекты функционирования цепи мы разобрали, так что давайте посмотрим, как она работает на практике. А для этого попробуем подавать на вход какой-нибудь сигнал и посмотрим, что получится на выходе. В качестве примера, подадим на вход последовательность прямоугольных импульсов:

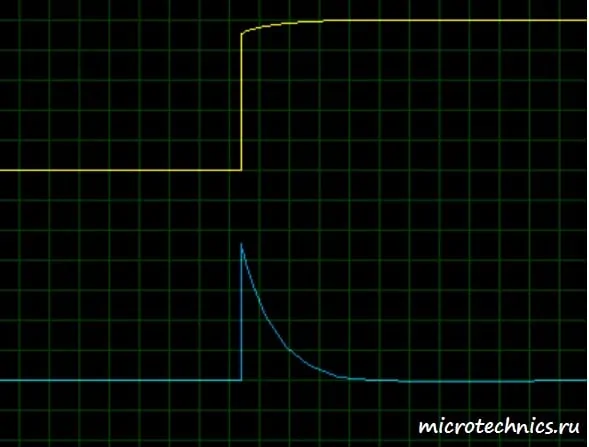
А вот как выглядит осциллограмма выходного сигнала (второй канал – синий цвет):

Что же мы тут видим?

Большую часть времени напряжение на входе неизменно, а значит его дифференцаил равен 0 (производная константы = 0). Именно это мы и видим на графике, значит цепь выполняет свою дифференцирующую функцию. А с чем же связаны всплески на выходной осциллограмме? Все просто – при “включении” входного сигнала происходит процесс зарядки конденсатора, то есть по цепи проходит ток зарядки и напряжение на выходе максимально. А затем по мере протекания процесса зарядки ток уменьшается по экспоненциальному закону до нулевого значения, а вместе с ним уменьшается напряжение на выходе, ведь оно равно $U_{out} = i R$ . Давайте увеличим масштаб осциллограммы и тогда мы получим наглядную иллюстрацию процесса зарядки:

При “отключении” сигнала на входе дифференцирующей цепи происходит аналогичный переходный процесс, но только вызван он не зарядкой, а разрядкой конденсатора:

В данном случае постоянная времени цепи у нас имеет небольшую величину, поэтому цепь хорошо дифференцирует входной сигнал. По нашим теоретическим расчетам, чем больше мы будем увеличивать постоянную времени, тем больше выходной сигнал будет похож на входной. Давай проверим это на практике 🙂

Будем увеличивать сопротивление резистора, что и приведет к росту $\tau$ :

Тут даже не надо ничего комментировать – результат налицо 🙂 Мы подтвердили теоретические выкладки, проведя практические эксперименты, так что давайте переходить к следующему вопросу – к интергрирующим RC-цепям.

Интегрирующая RC-цепь.

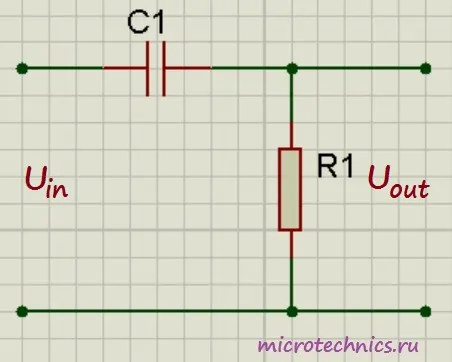
Запишем выражения для вычисления тока и напряжения данной цепи:

$i = C \frac{du_{out}}{dt}$

В то же время ток мы можем определить из Закона Ома:

$i = \frac{u_R}{R} = \frac{u_{in} - u_{out}}{R}$

Приравниваем эти выражения и получаем:

$C \frac{du_{out}}{dt} = \frac{u_{in} - u_{out}}{R}$

$du_{out} = \frac{1}{C} \frac{u_{in} - u_{out}}{R} dt$

Проинтегрируем правую и левую части равенства:

$u_{out} = \frac{1}{R C} \int(u_{in} - u_{out}) dt = \frac{1}{R C} \int(u_{in}) dt - \frac{1}{R C} \int(u_{out}) dt$

Как и в случае с дифференцирующей RC-цепочкой здесь возможны два случая:

Если $u_{out} << \frac{1}{R C} \int(u_{out}) dt$ , то $\frac{1}{R C} \int(u_{in}) dt - \frac{1}{R C} \int(u_{out}) dt \approx 0$ и, соответственно, $U_{out} \approx dU_{in}$ . То есть сигнал на выходе приближенно повторяет входной сигнал. Для выполнения этого условия необходимо, чтобы постоянная времени цепи имела малую величину.
Если $u_{out} >> \frac{1}{R C} \int(u_{out}) dt$ , то $u_{out} \approx \frac{1}{R C} \int(u_{in}) dt$ . В данном случае цепь хорошо выполняет свою интегрирующую функцию, и чем больше будет величина постоянной времени цепи, тем интегрирующие свойства будут лучше.

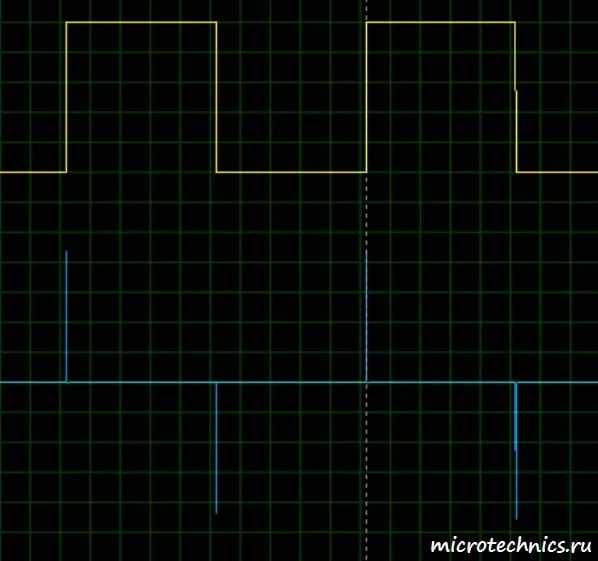
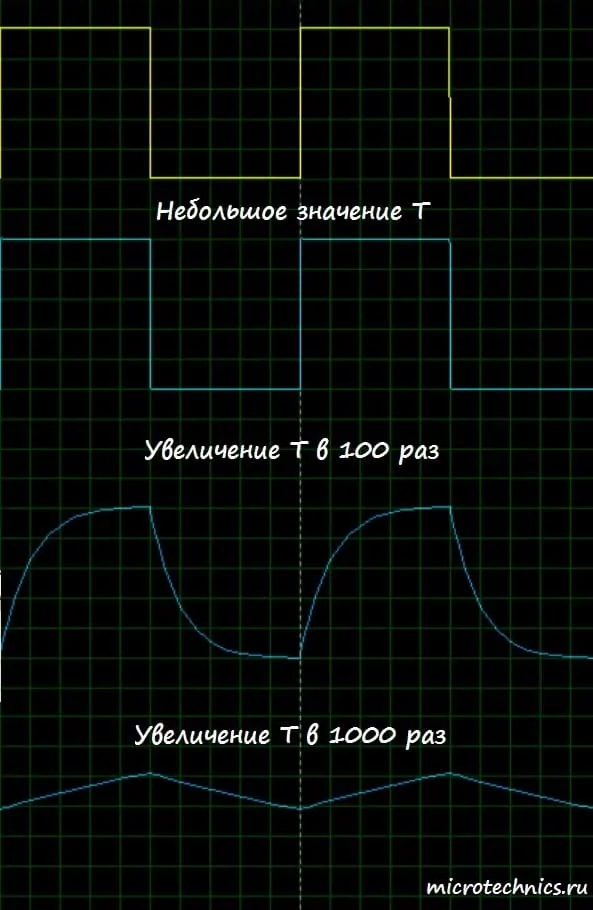
Для того, чтобы убедиться в работоспособности цепи, давайте подадим на ее вход точно такой же сигнал, какой мы использовали при анализе работы дифференцирующей цепи, то есть последовательность прямоугольных импульсов. При малых значениях $\tau$ сигнал на выходе будет очень похож на входной сигнал, а при больших величинах постоянной времени цепи, на выходе мы увидим сигнал, приближенно равный интегралу входного. А какой это будет сигнал? Последовательность импульсов представляет собой участки равного напряжения, а интеграл от константы представляет из себя линейную функцию ( $\intC dx = C x$ ). Таким образом, на выходе мы должны увидеть пилообразное напряжение. Проверим теоретические выкладки на практике:

Желтым цветом здесь изображен сигнал на входе, а синим, соответственно, выходные сигналы при разных значениях постоянной времени цепи. Как видите, мы получили именно такой результат, который и ожидали увидеть 🙂

На этом мы и заканчиваем сегодняшнюю статью, но не заканчиваем изучать электронику, так что до встречи в новых статьях! 🙂

Дифференцирующие и интегрирующие RC-цепи.: 13 комментариев

Chettuser говорит 01.08.2016 в 23:34:

Было бы неплохо ещё про LR-цепи рассказать. Понимаю, что они применяются реже, но всё же…

Ответить ↓
- Aveal говорит 09.08.2016 в 21:12:
  
  Постараюсь, но не обещаю..
  
  Ответить ↓
Владимир говорит 12.08.2017 в 12:24:

Почему при положительном скачке в дифференцирующей цепи он заряжается мгновенно, а разряжается не мгновенно?
(третья картинка с осциллографа).

Ответить ↓
- Aveal говорит 12.08.2017 в 15:03:
  
  На третьей картинке у нас при подаче напряжения на вход начинает заряжаться конденсатор. В начальный момент ток (i) максимален, а затем начинает уменьшаться. Это мы и видим не осциллограмме – Uout = i * R. Или я не совсем понял вопрос?
  
  Ответить ↓
Alex говорит 20.12.2017 в 08:42:

Так все же чем дифференциальная схема отличается от интегрирующей

Ответить ↓
- vladk говорит 26.01.2018 в 07:05:
  
  Дифференциальная схема отличается от интегрирующей существенными, я бы даже сказал принципиальными, отличиями, которые подробно рассмотрены в статье.
  
  Ответить ↓
Евгений говорит 28.06.2018 в 21:52:

В нескольких местах встретил: Uout приблизительно равен dUin. Т.е. выходное напряжение приблизительно равно дифференциалу входного? Не лишний ли здесь знак дифференциала?

Ответить ↓
- Aveal говорит 28.06.2018 в 23:01:
  
  Поправил, спасибо!
  
  Ответить ↓
сергей говорит 18.08.2018 в 20:47:

ВСЁ ПРАВИЛЬНО И ЧЁТКО СКАЗАНО! СПАСИБО ! НАПОМНИЛ!!! надо задержки включения и выключения делать вот и поглядел.вспомнил! спасибо!

Ответить ↓
сергей говорит 18.08.2018 в 20:54:

именно на интегрирующих и дифференцирующих цепочках легко делать задержку включения сигналки…….время отработки её..да и так далее!!! СПАСИБО ЕЩЁ РАЗ

Ответить ↓
- Aveal говорит 20.08.2018 в 13:02:
  
  Спасибо за отличный отзыв!!!
  
  Ответить ↓
Денис говорит 30.05.2019 в 19:11:

У вас для интегрирующей RC в выражении dUout лишняя R в знаменатели

Ответить ↓
- Aveal говорит 30.05.2019 в 22:51:
  
  Исправил, огромное спасибо за замечание!!!
  
  Ответить ↓