Продолжаем начатую тему, посвященную работе ПИД-регулятора, и сегодня речь пойдет непосредственно и исключительно о настройке ПИД-регулятора. Начнем, как полагается, с теоретических моментов, затем же плавно перейдем к практическому примеру на базе регулятора температуры на STM32, созданному нами в той, первой, статье.
Настройка ПИД-регулятора. Теория.
И, собственно, данная настройка заключается в том, чтобы вычислить или подобрать оптимальные значения коэффициентов:
- K_p - коэффициент усиления пропорциональной составляющей
- K_i - коэффициент усиления интегрирующей составляющей
- K_d - коэффициент усиления дифференцирующей составляющей
По большому счету, при использовании ПИД-регулятора необходимо построить модель всей системы в целом и математически вычислить необходимые значения коэффициентов. В таком случае значения можно рассчитать очень точно. Но на практике математический расчет коэффициентов - задача далеко не тривиальная и требует глубоких знаний теории автоматического управления, поэтому в большинстве случаев используются другие, упрощенные, методы настройки.
Существует целый ряд различных способов, которые определяют вполне конкретные шаги, которые необходимо предпринимать. Мы же разберем один из них, а именно - метод Циглера-Никольса, ввиду того, что он получил наибольшее распространение и популярность.
Метод Циглера-Никольса.
Заключается он в последовательном выполнении следующих операций:
- Обнуляем все коэффициенты регулятора.
- Задаем некоторое целевое значение регулируемого параметра (например, температуры).
- Постепенно начинаем увеличивать пропорциональный коэффициент и следим за реакцией системы.
- При определенном значении K_p возникнут незатухающие колебания регулируемой величины.
- Фиксируем это значение, а также период колебаний системы.
На этом практическая часть метода заканчивается. Из полученных значений рассчитываем коэффициенты:
K_p = 0.6\cdot K \\ K_i = (2\cdot K_p)\medspace/\medspace T \\ K_d = (K_p\cdot T)\medspace/\medspace 8
Здесь K – тот самый коэффициент пропорциональной составляющей, при котором возникли колебания, а T – период этих колебаний. Рассмотрим псевдо-пример для получения более полного представления о данном процессе. Пусть при K_p равном 10, возникают колебания следующего рода:
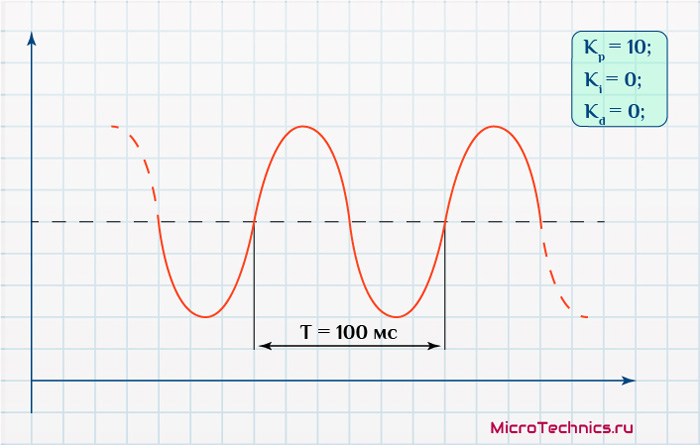
Период составляет 0.1 с. Производим расчеты по вполне конкретным формулам и получаем:
K_p = 0.6\cdot 10 = 6 \\ K_i = (2\cdot 6)\medspace/\medspace 0.1 = 120 \\ K_d = (6\cdot 0.1)\medspace/\medspace 8 = 0.075
Все, на этом процедура окончена.
Метод довольно прост, но применить его можно далеко не всегда. И получаемые результаты также будут оптимальными далеко не всегда. На практике я метод Циглера-Никольса применял считанное число раз, больше доверяясь экспериментально-аналитическому способу, которому и буде посвящена последующая часть статьи.
Суть метода можно описать максимально кратко:
- Берем систему.
- Меняем один из коэффициентов.
- Смотрим за реакцией системы.
- Анализируем произошедшее и принимаем решение о дальнейших действиях.
Данный метод также вполне можно назвать «методом проб и ошибок», тем не менее это работает. Главное иметь представление о том, как система функционирует и как она реагирует на изменения, чтобы производимые манипуляции не носили хаотичный, близкий к случайному характер. Кроме того, не следует менять несколько значений сразу, тогда отслеживание результата становится практически неосуществимым. Поменяли-посмотрели-поменяли-посмотрели…
Сами значения коэффициентов могут принимать абсолютно разные значение, от 0 до десятков-сотен тысяч. Это все зависит, в первую очередь, от конкретной системы, и следует даже просто из того, что регулируемые и регулирующие параметры могут быть абсолютно разными.
Пусть, к примеру, у нас температура может меняться от 20°C до 40°C, при этом мощность нагревателя – от 100 Вт до 1000 Вт. Это частный случай. Берем абсолютно другую систему, там ПИД-регулятор контролирует угол наклона гиростабилизированной платформы. Объект регулирования – угол наклона, выходное воздействие – сигнал для управления двигателем, вращающим платформу. При этом рабочий диапазон углов: [-0.1°; 0.1°]. То есть изначально мы имеем абсолютно другие порядки участвующих в работе системы параметров, соответственно, и коэффициенты ПИД-регулятора могут иметь значения, разнящиеся на несколько порядков.
Перечислим еще некоторые свойства, которые призваны помочь в анализе работы системы и настройке ПИД-регулятора:
- Увеличение коэффициента усиления пропорциональной составляющей приводит к увеличению быстродействия, но снижению устойчивости системы.
- Интегральная составляющая служит для уменьшения статической ошибки, о чем мы говорили в предыдущей статье. При увеличении K_i компенсация ошибки будет происходить быстрее.
- Увеличение K_d позволяет повысить стабильность системы, но слишком большое значение может также стать причиной возникновения колебаний, поэтому, как и для остальных коэффициентов, нужно все манипуляции производить аккуратно и в меру.
Не для всех систем целесообразно использовать все три составляющие, иногда достаточно и нескольких из них. Собственно, на этой ноте переходим к практическому примеру настройки ПИД-регулятора. Произведем базовую, максимально наглядную, настройку, дабы получить в первом приближении нормально функционирующую систему. Система крайне инертная и медленная по своей сути, так что можно столкнуться с проблемами, напоминаю структурную схему творения:
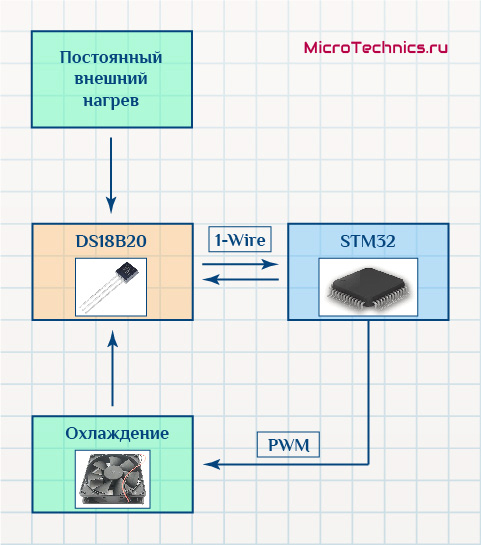
Пример настройки ПИД-регулятора на микроконтроллере STM32.
Итак, проект мы создали в первой части, сейчас же целенаправленно займемся настройкой значений:
float Kp = 0; float Ki = 0; float Kd = 0;
На данный момент все коэффициенты в нуле, то есть регулятор не функционирует. Начинаем последовательно производить настройку описанным экспериментально-аналитическим способом. Прикинем возможные диапазоны значений. Итак, пусть невязка (разница между текущим значением температуры и целевым) равна 1°C. Выходной сигнал может изменяться от 0 до 1000 (длительность импульсы ШИМ-сигнала для управления охлаждением). Если поставим K_p равным 100, то на это значение невязки получим длительность импульса выходного ШИМ-сигнала равной 100, вполне адекватное значение.
Для анализа поведения системы будем производить следующее:
- Задаем целевое значение 30°C, ждем пока система стабилизируется.
- Задаем целевое значение 40°C, аналогично ожидаем эффекта.
- Строим график зависимости температуры датчика от времени и анализируем полученное.
Приступаем, тест №1:
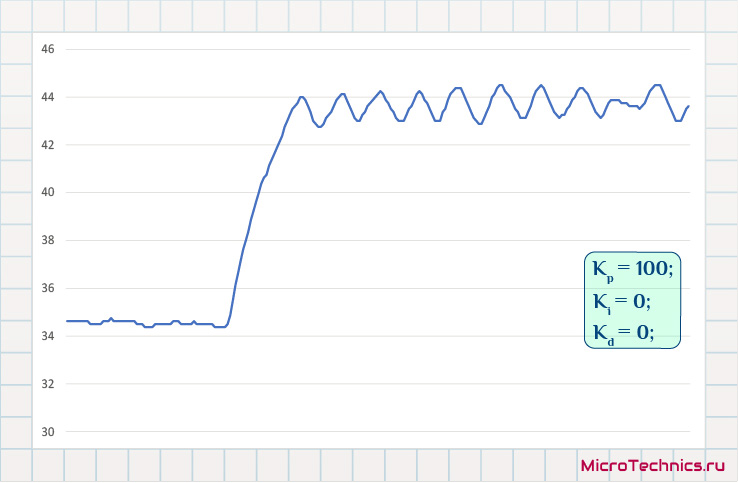
Видим, что все точно в соответствии с теорией – при использовании только пропорциональной составляющей система не может выйти на требуемые значения из-за статической ошибки. Отлично, добавим интегрирующую составляющую, задав некоторое значение K_i:
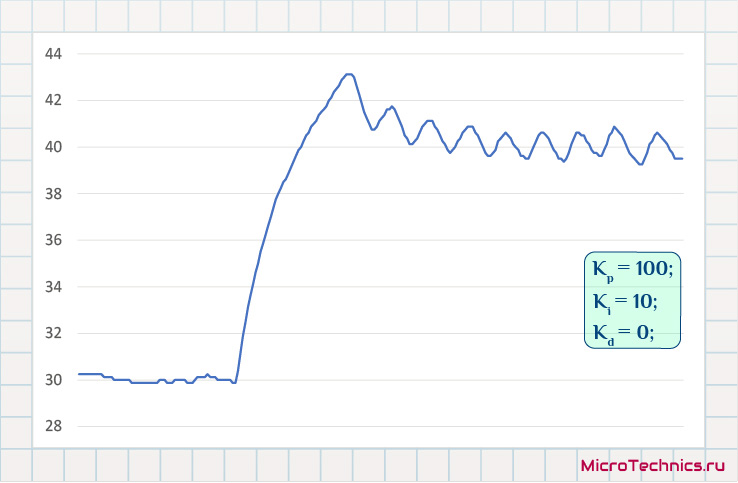
На этот раз уже все иначе – целевое значение более-менее установить удается, но имеем неслабый выброс при подходе к значению. Логичным шагом будет увеличение коэффициента усиления дифференцирующей составляющей:
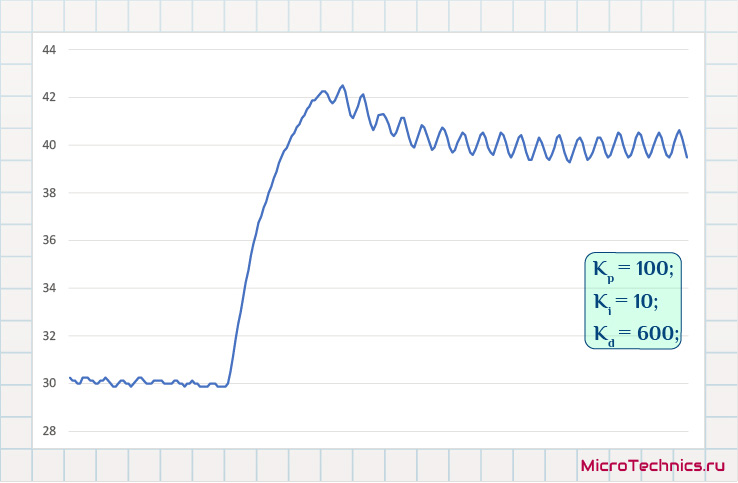
Так, стало получше (амплитуда выброса уменьшилась), увеличиваем K_d еще:
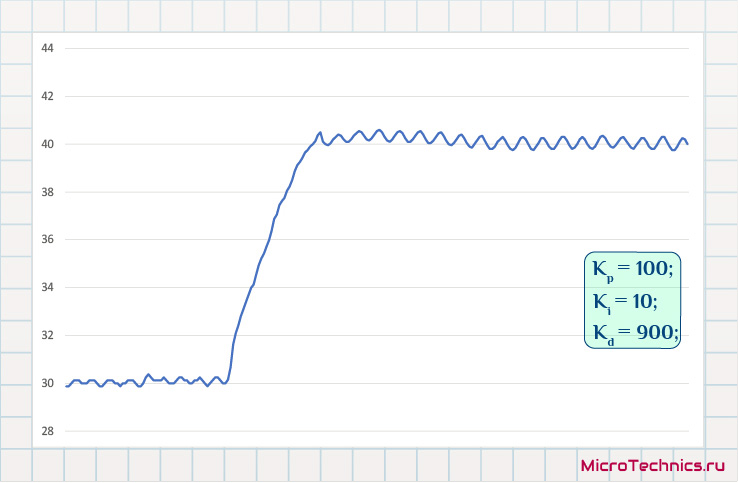
Отлично, выброс практически погасили, но выходить на нужное значение хотелось бы побыстрее. Вывод очевиден – увеличиваем коэффициент усиления пропорциональной составляющей (K_p):
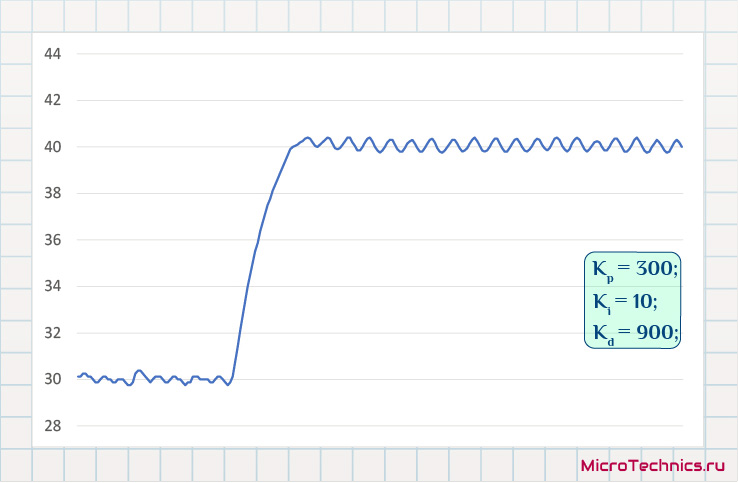
Вот, намного приятнее, посмотрим на последние два варианта друг относительно друга:
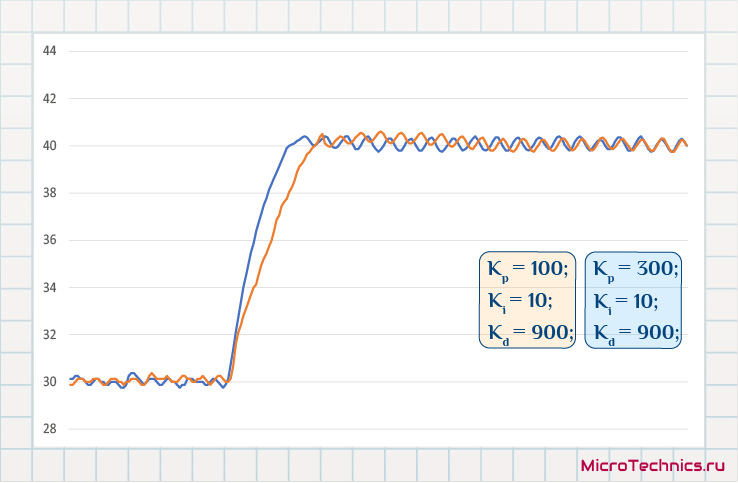
Вполне себе ничего результат в итоге. Опять же система очень инертная изначально, датчик производит измерения не слишком быстро, да и шаг дискретизации приличный - 0.125 °C. Так что результат вполне годный. Наблюдаемые промежуточные графики очень хорошо демонстрируют суть протекающих процессов, а это и было нашей целью – получение наглядного примера, дополняющего рассмотренные теоретические аспекты. Так что на этом заканчиваем на сегодня, следите за обновлениями и спасибо за внимание 🤝
Ссылка на проект - MT_PID_Project.
