Сегодняшняя статья будет посвящена такой замечательной вещи как ПИД-регулятор. По определению, пропорционально-интегрально-дифференцирующий регулятор - это устройство в цепи обратной связи, используемое для поддержания заданного значения измеряемого параметра. Довольно часто можно встретить примеры, где ПИД-регулятор используется для регулировки температуры, и, на мой взгляд, этот пример прекрасно подходит для изучения теории и понимания принципов работы. Поэтому именно ПИД-регулятор температуры сегодня и будем рассматривать. Начнем с обзора теоретических нюансов, а финишируем все это реальным практическим примером для микроконтроллеров STM32. Во второй же, отдельной, статье рассмотрим настройку регуляторов, причем опять же как теорию, так и реальный пример.
Принцип работы ПИД-регулятора.
Итак, что у нас имеется? Разбираем на примере регулятора температуры:
- Во-первых, объект, температуру которого необходимо поддерживать на заданном уровне.
- Во-вторых, некое внешнее воздействие, которое и будет задавать требуемую температуру (ПК на схеме).
- Собственно, элемент, тем или иным способом производящий регулировку температуры, к примеру, охлаждающая система или непосредственно нагреватель.
- Работой этого элемента нужно как-то управлять, хоть с помощью того же микроконтроллера, почему нет.
- Ну и помимо регулирования необходимо знать текущее значение параметра, в данном контексте - значение температуры.
Все это можно изобразить на структурной схеме следующего вида:
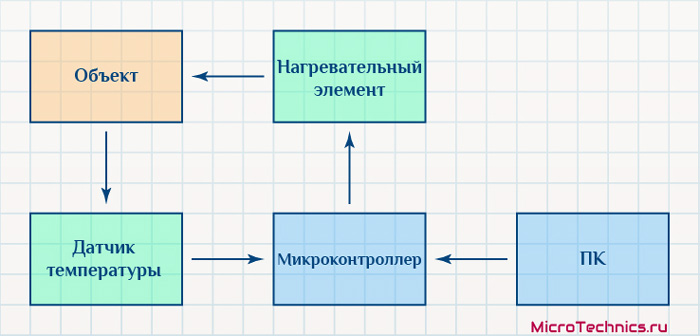
Соответственно, элементы могут быть абсолютно разными, характеристики и параметры тоже, но суть и принцип работы ПИД-регулятора неизменны. К разбору этого сейчас и перейдем.
Итак, фактически у нас имеются в наличии входные данные:
- Текущая температура, полученная с измерительной системы (датчика).
- Целевая температура, заданная управляющей системой.
Необходимо обеспечить, чтобы температура объекта была равна целевому значению. То есть в идеале задача сводится к следующему:
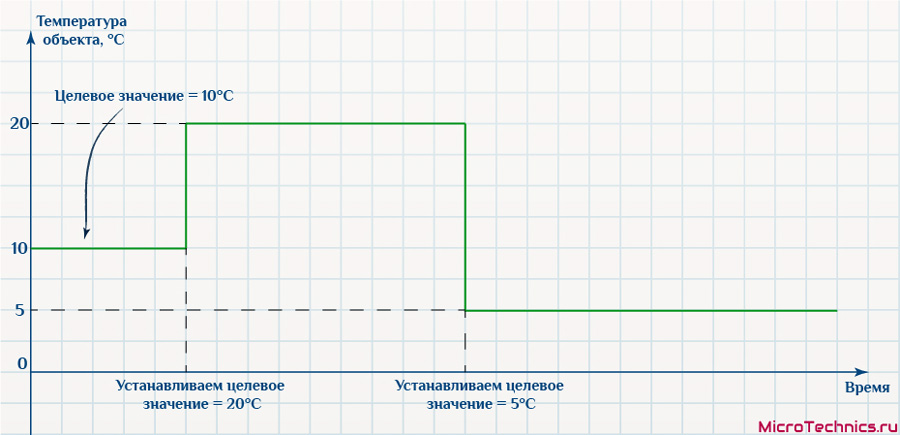
На практике чаще всего такого добиться не получится, поскольку ничто не идеально, даже ПИД-регулятор. И результат может быть следующим:
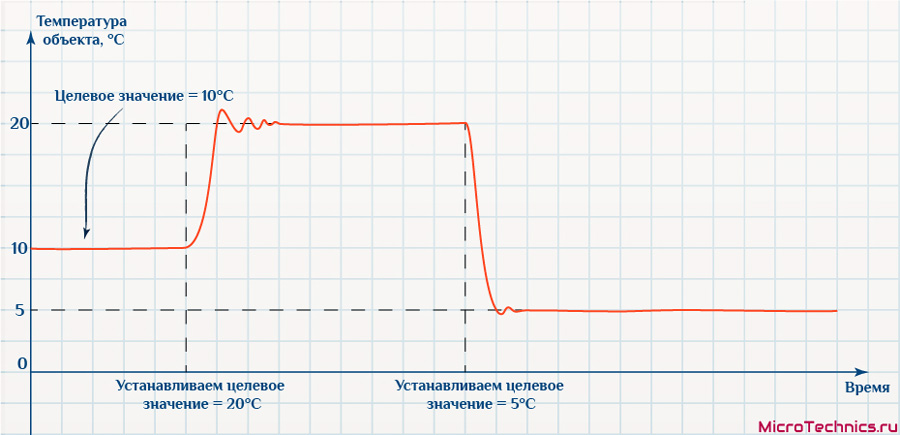
Графическое представление значений для реальной системы мы увидим при разработке практического примера во второй части. А пока продолжим, с задачей регулирующей деятельности все понятно, двигаемся дальше.
А дальше необходимо как-то менять текущую температуру, для чего на схеме и присутствует нагреватель. Увеличивая мощность, подаваемую на него, обеспечиваем нагрев, что эквивалентно увеличению температуры. Аналогично, уменьшая мощность, имеем охлаждение ⇒ уменьшение температуры объекта.
Пока не ясно, зачем вообще нужен какой-то специфичный регулятор, если все управляется так логично и однозначно, но как раз к сути этого вопроса мы и подобрались вплотную.
А суть эта, заключается в том, что нет конкретного математического способа, позволяющего из целевого значения температуры вычислить конкретное же значение мощности, которую необходимо передать на нагреватель (для данного примера). Да, конечно, можно провести исследования и получить ряд значений (все значения выдуманы и любое совпадение с реальными является случайным😉):
| Температура объекта | Мощность нагревательного элемента |
|---|---|
| 25°C | 100 Вт |
| 27.5°C | 125 Вт |
| 30°C | 150 Вт |
| 32.5 | 175 Вт |
| 35°C | 200 Вт |
| 37.5°C | 225 Вт |
| 40°C | 250 Вт |
Более того, вполне вероятно, что для конкретной системы зависимость может быть максимально простой - линейной. Но! Это все имеет место для идеализированной теоретической системы. В реальности все не так, и при изменении какого-либо внешнего фактора или факторов работу такой системы (использующей предрассчитанные значения) постигнет крах.
Вернемся снова к нашему конкретному примеру с ПИД-регулятором температуры. Пусть мы подобрали, например, что значению 35°C соответствует мощность нагревателя, равная 200 Вт. При этом данный результат мы получили при температуре окружающей среды 25°C. Очевидно, что как только T_{окр \medspace ср} станет иной, все эти расчеты перестанут давать ожидаемый результат.
В этом и заключается смысл использования ПИД-регулятора для задач такого рода. А именно в том, что он обеспечит регулировку параметра независимо от изменения внешних неконтролируемых факторов. Математически принцип работы можно представить очень просто:
y(t) = f(e(t))
Здесь:
- y(t) - выходной сигнал.
- e(t) - разность между целевым и текущим значением регулируемого параметра.
И ПИД-регулятор дает нам механизм для расчета y(t) из e(t). Снова ссылаюсь на будущий пример, в котором все окончательно встанет на свои места. А пока планомерно перемещаемся к рассмотрению того, как именно происходят данные вычисления. Выходной сигнал регулятора определяется так:
y(t) = P + I + D = K_p \cdot e(t) + K_i \cdot \int_0^t e(\tau) d\tau + K_d \cdot \frac{de}{dt} Имеем алгебраическую сумму трех составляющих, которые и дали название регулятору - ПИД:
- e(t) - пропорциональная составляющая
- \int_0^t e(\tau) d\tau - интегрирующая
- \frac{de}{dt} - дифференцирующая
Сразу стоит отметить, что могут использоваться не все составляющие, а только часть из них, тогда регулятор будет называться пропорционально-дифференцирующим, пропорционально-интегрирующим и т. д. Логика формирования названий тут проста и очевидна.
Формула имеет три неопределенные величины, в подборе которых и заключается настройка ПИД-регулятора. Речь о коэффициентах усиления пропорциональной, интегрирующей и дифференцирующей составляющих (K_p, K_i, K_d).
Рассмотрим физический смысл упомянутых параметров. Начнем с пропорциональной составляющей. Здесь все просто, берем значение нужной нам температуры (так называемую уставку) и вычитаем из него значение текущей температуры. Получаем рассогласование (невязку). Умножаем полученную невязку на коэффициент и получаем значение мощности, которое и передаем на нагреватель.
Но при использовании только пропорциональной составляющей есть ряд проблем, в частности, влияние статической ошибки. Статической ошибкой называется такое отклонение регулируемого параметра, при котором выходное воздействие имеет величину, которая стабилизирует систему на этом текущем значении. Рассмотрим для понимания на конкретном примере все того же ПИД-регулятора температуры. Допустим:
- Целевое значение температуры равно 20°C.
- Текущее значение - 10°C.
- Температура окружающей среды - 15°C.
- Коэффициент K_p - 10, остальные коэффициенты нулевые, поскольку рассматриваем случай использования только пропорциональной составляющей.
Итак, производим расчет выходного сигнала:
y(t) = P + I + D = 10 \cdot (20-10) + 0 + 0 = 100 \medspace Вт
Таким образом, при заданных значениях получаем мощность нагревателя, равную 100 Вт. Собственно, подаем это значение на нагреватель, что приводит к тому, что температура объекта начинает увеличиваться. Вместе с этим ростом получаем уменьшение невязки (e(t) = T_{цел} - T_{тек}), которое напрямую ведет к уменьшению мощности нагревателя.
И в результате имеем стабилизацию системы на некотором значении, к примеру, на текущей температуре в 17°C. При этом значении на нагреватель подается:
y(t) = P + I + D = 10 \cdot (20-17) + 0 + 0 = 30 \medspace Вт
При этом идет теплообмен с окружающей средой. Дальнейший рост температуры снова приводит к уменьшению мощности, выдаваемой на нагреватель, что ведет уже напротив к уменьшению текущей температуры. Таким образом, при определенном значении наступает баланс между теплом, которое дает объекту нагреватель и теплом, которое отдается в окружающую среду.
В случае одной только пропорциональной составляющей на данном этапе наступает коллапс, и система дальнейшей регулировке не поддается, температура не может достичь целевого значения. Увеличение коэффициента K_p может приводить к уменьшению статической ошибки, но в определенный момент это увеличение приведет к возникновению автоколебаний, из чего прямо следует потеря системой устойчивости.
Как раз для устранения в красках описанного нежелательного эффекта и используется интегрирующая составляющая. Снова обращаемся к реальной ситуации для максимальной наглядности. Пусть температура ниже значения уставки, нагреватель начинает ее увеличивать. Пока идет нагрев, значение невязки положительное и накапливается в интегрирующей составляющей. Когда температура дошла до нужного значения, пропорциональная и дифференцирующая составляющие стали равны нулю, а интегрирующая перестала изменяться, но ее значение не стало нулевым. Таким образом, благодаря накопленному значению интегрирующей составляющей мы продолжаем выдавать мощность, и нагреватель поддерживает целевое значение температуры, не давая объекту охлаждаться.
Дифференцирующая же составляющая противодействует предполагаемым отклонениям регулируемой величины, которые могут произойти в будущем.
Итак, пусть снова у нас текущая температура ниже целевого значения. Пропорциональная и интегрирующая составляющие обеспечивают выдачу мощности на нагреватель. Дифференцирующая составляющая вносит свой вклад в мощность и представляет из себя производную невязки, взятую также с определенным коэффициентом. Температура растет и приближается к нужному значению, а следовательно невязка в предыдущий момент больше текущего значения невязки, и производная - отрицательная. Таким образом, дифференцирующая составляющая начинает постепенно снижать мощность до того, как температура достигла необходимого значения.
Вот во всем вышеописанном и заключается концепция и принцип работы ПИД-регулятора. А мы тем временем переходим к практическому примеру.
ПИД-регулятор температуры на микроконтроллере STM32.
Итак, поставив задачу найти максимально простейшие элементы и покопавшись на полках, я подобрал все необходимые узлы:
- Высокотехнологичное охлаждающее устройство, цена 120 р.:

- Отладочная плата на базе STM32F401CC:

- Датчик температуры DS18B20 в составе модуля KY-001.
Плюс добавлю дополнительный постоянный внешний нагрев:
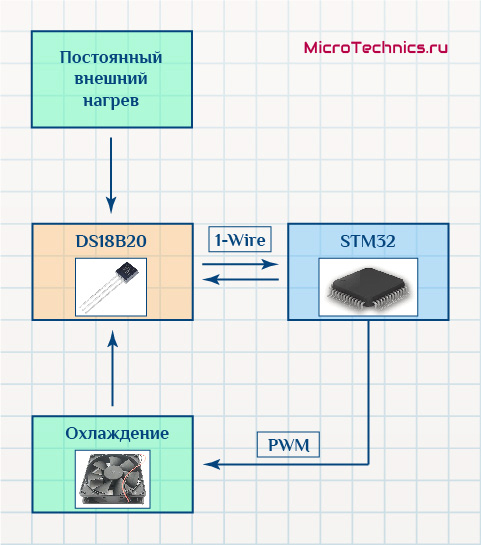
Задачей ПИД-регулятора будет обеспечение температуры датчика, равной целевому значению, которое будем задавать программно. Непосредственно регулировка будет происходить изменением скорости вращения вентилятора, путем изменения скважности ШИМ-сигнала. Подключаем через ключ на транзисторе:
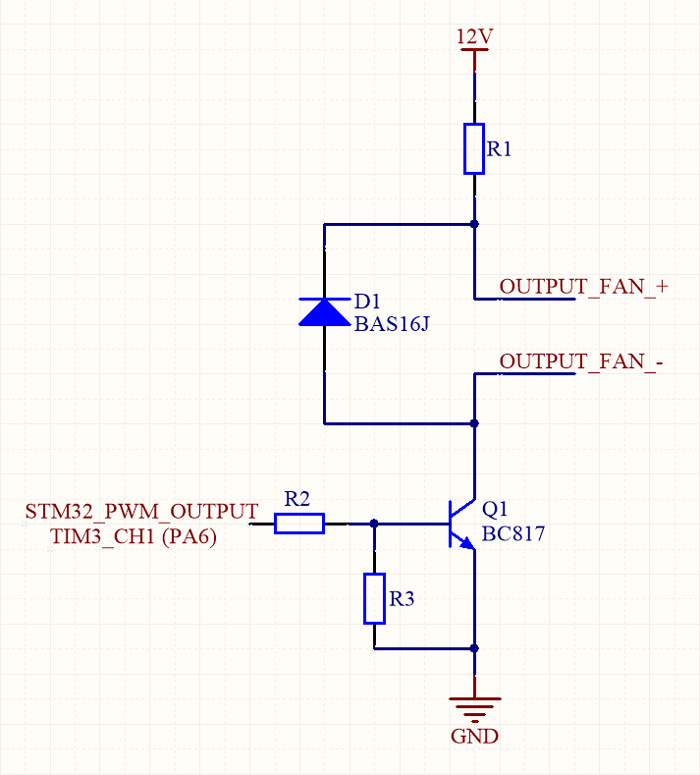
Переходим к созданию проекта для STM32. Ввиду популярности среди читателей блога я текущие проекты для сайта делаю в STM32CubeIDE, будет так и в этот раз, так что конфигурируем базово-необходимую периферию (мы это проделываем в каждом проекте, поэтому отдельно углубляться не буду):
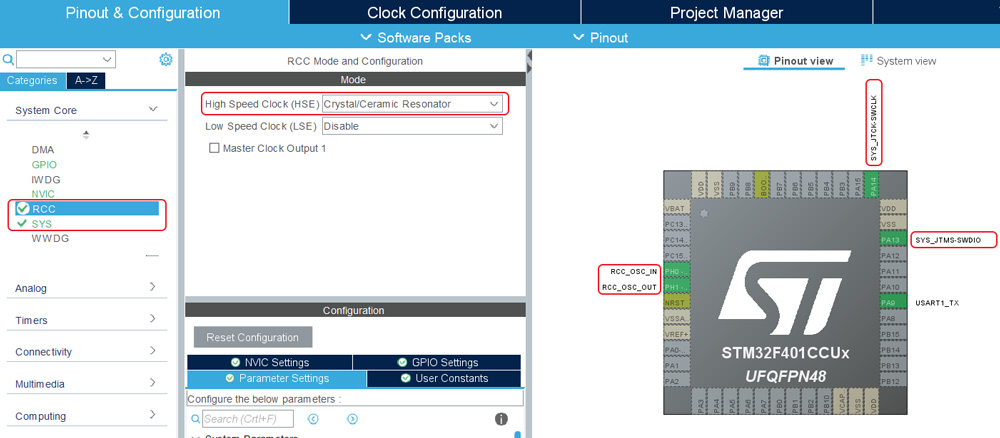
Настройки тактирования:
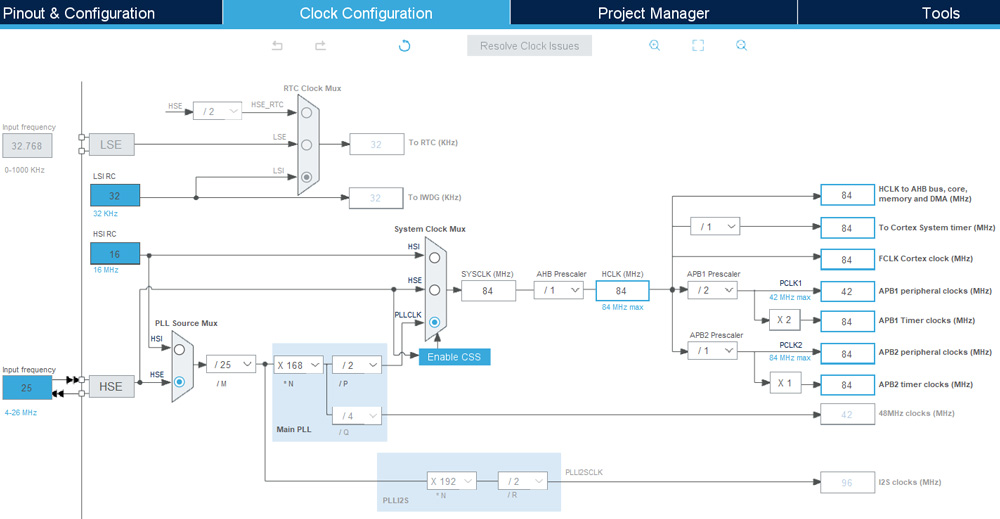
Непосредственно для данной задачи нам нужны USART1 для обмена данными с датчиком температуры, а также один канал ШИМ для управления вентиляционной деятельностью:
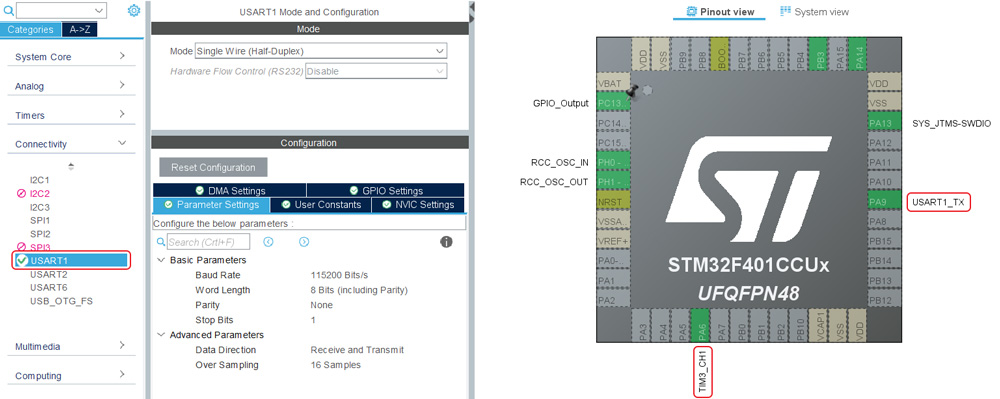
Буквально в одной из предыдущих статей написали библиотеки для работы с 1-Wire и DS18B20, так что естественно их и задействуем.
Таймер же настроим на период, равный 1 мс, длительность импульса будем менять от нуля до этой самой одной миллисекунды. Чем больше длительность, тем сильнее вращение вентилятора ⇒ больше охлаждение датчика. И, кроме того, включаем прерывание по переполнению таймера:
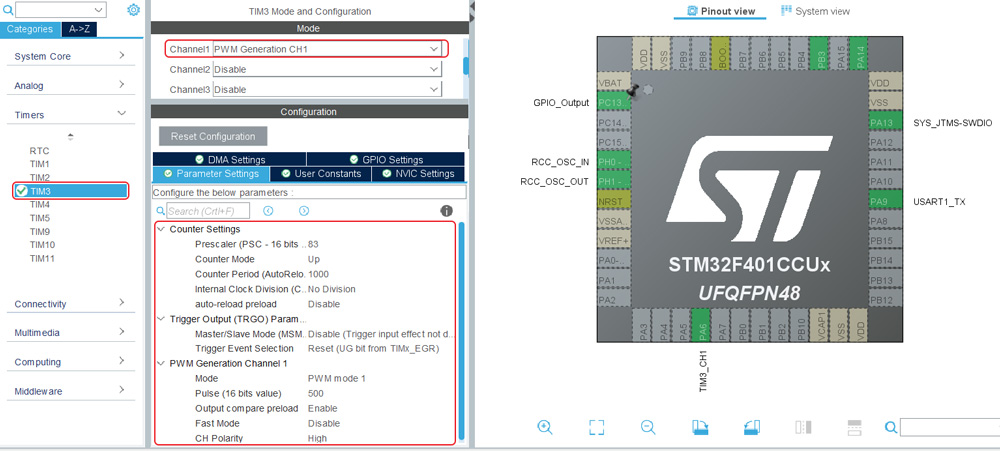
На форуме была тема, посвященная данной конфигурации, поэтому в main.c после непосредственно запуска таймера добавляем:
HAL_TIM_PWM_Start_IT(&htim3, TIM_CHANNEL_1); __HAL_TIM_ENABLE_IT(&htim3, TIM_IT_UPDATE);
Итак, работу с датчиком построим точно так же, как в многократно упомянутой статье, поэтому имеем в результате:
/* Initialize all configured peripherals */
MX_GPIO_Init();
MX_USART1_UART_Init();
MX_TIM3_Init();
/* USER CODE BEGIN 2 */
DS18B20_Init(&temperatureSensor, &huart1);
DS18B20_InitializationCommand(&temperatureSensor);
DS18B20_ReadRom(&temperatureSensor);
DS18B20_ReadScratchpad(&temperatureSensor);
uint8_t settings[3];
settings[0] = temperatureSensor.temperatureLimitHigh;
settings[1] = temperatureSensor.temperatureLimitLow;
settings[2] = DS18B20_11_BITS_CONFIG;
DS18B20_InitializationCommand(&temperatureSensor);
DS18B20_SkipRom(&temperatureSensor);
DS18B20_WriteScratchpad(&temperatureSensor, settings);
HAL_TIM_PWM_Start_IT(&htim3, TIM_CHANNEL_1);
__HAL_TIM_ENABLE_IT(&htim3, TIM_IT_UPDATE);
/* USER CODE END 2 */
/* Infinite loop */
/* USER CODE BEGIN WHILE */
while (1)
{
/* USER CODE END WHILE */
/* USER CODE BEGIN 3 */
DS18B20_InitializationCommand(&temperatureSensor);
DS18B20_SkipRom(&temperatureSensor);
DS18B20_ConvertT(&temperatureSensor, DS18B20_DATA);
DS18B20_InitializationCommand(&temperatureSensor);
DS18B20_SkipRom(&temperatureSensor);
DS18B20_ReadScratchpad(&temperatureSensor);
}
/* USER CODE END 3 */
}
В данном случае разрешение датчика устанавливаем равным 11 бит. А в основном цикле программы ведем постоянный опрос текущей температуры. Вся оставшаяся работа, которую необходимо выполнить, заключается уже в реализации ПИД-регулятора и только в этом.
Начнем с того, что добавим необходимые переменные:
float pwmDutyCycle = 500; float Kp = 0; float Ki = 0; float Kd = 0; float errorPrevious = 0; float errorCurrent = 0; float errorIntegral = 0; float errorDifferential = 0; uint32_t timeCounterMs = 0; float targetTemperature = 30; /* USER CODE END PV */
pwmDutyCycle- длительность импульса ШИМ-сигнала. Период сигнала в «тиках» таймера равен 1000, соответственно данный параметр может принимать значения от 0 до 1000.Kp,Ki,Kd- коэффициенты ПИД-регулятора.errorPrevious,errorCurrent- предыдущее и текущее значения невязки, то есть разницы между текущим значением температуры и целевым.errorIntegral,errorDifferential- значения интегрирующей и диффиренцирующей составляющих.timeCounterMs- счетчик миллисекунд.targetTemperature- и, наконец, целевая температура, ее значение будем менять под отладчиком и следить за реакцией системы.
Следующим шагом добавляем обработчик прерывания по переполнению таймера, в котором обновляем значение длительности импульса генерируемого сигнала, а также инкрементируем введенный счетчик миллисекунд:
/* USER CODE BEGIN 4 */
void HAL_TIM_PeriodElapsedCallback(TIM_HandleTypeDef *htim)
{
if (htim == &htim3)
{
TIM3->CCR1 = (uint16_t)pwmDutyCycle;
timeCounterMs++;
}
}
/* USER CODE END 4 */
Все, теперь добавляем в основной цикл кусок, посвященный работе ПИД-регулятора температуры:
while (1)
{
/* USER CODE END WHILE */
/* USER CODE BEGIN 3 */
DS18B20_InitializationCommand(&temperatureSensor);
DS18B20_SkipRom(&temperatureSensor);
DS18B20_ConvertT(&temperatureSensor, DS18B20_DATA);
DS18B20_InitializationCommand(&temperatureSensor);
DS18B20_SkipRom(&temperatureSensor);
DS18B20_ReadScratchpad(&temperatureSensor);
float timeCounterSec = (float)timeCounterMs / 1000;
errorCurrent = temperatureSensor.temperature - targetTemperature;
if ((((Ki * errorIntegral) <= PID_DUTY_CYCLE_MAX) && (errorCurrent >= 0)) ||
(((Ki * errorIntegral) >= PID_DUTY_CYCLE_MIN) && (errorCurrent < 0)))
{
errorIntegral += errorCurrent * timeCounterSec;
}
errorDifferential = (errorCurrent - errorPrevious) / timeCounterSec;
pwmDutyCycle = Kp * errorCurrent + Ki * errorIntegral + Kd * errorDifferential;
if (pwmDutyCycle < PID_DUTY_CYCLE_MIN)
{
pwmDutyCycle = PID_DUTY_CYCLE_MIN;
}
if (pwmDutyCycle > PID_DUTY_CYCLE_MAX)
{
pwmDutyCycle = PID_DUTY_CYCLE_MAX;
}
errorPrevious = errorCurrent;
timeCounterMs = 0;
}
/* USER CODE END 3 */
Пройдемся поэтапно и подробно.
Я ввел здесь дополнительное ограничение для интегрирующей составляющей для того, чтобы не происходило накопление слишком больших значений, что может привести к повышенной инертности системы:
float timeCounterSec = (float)timeCounterMs / 1000;
errorCurrent = temperatureSensor.temperature - targetTemperature;
if ((((Ki * errorIntegral) <= PID_DUTY_CYCLE_MAX) && (errorCurrent >= 0)) ||
(((Ki * errorIntegral) >= PID_DUTY_CYCLE_MIN) && (errorCurrent < 0)))
{
errorIntegral += errorCurrent * timeCounterSec;
}
Если текущая ошибка положительна, и при этом значение интегрирующей составляющей не превышает максимального значения длительности импульса ШИМ-сигнала, то производим накопление ошибки в errorIntegral, иначе не производим. Аналогично и для отрицательного значения ошибки.
Далее производим дифференцирование невязки четко по той логике, которую мы обсудили в теоретической части:
errorDifferential = (errorCurrent - errorPrevious) / timeCounterSec;
И все по той же неизменной логике рассчитываем выходное воздействие:
pwmDutyCycle = Kp * errorCurrent + Ki * errorIntegral + Kd * errorDifferential;
Вот и все, далее просто проверяем, что значение не вышло за пределы, определенные в:
/* USER CODE BEGIN PD */ #define PID_DUTY_CYCLE_MIN 0 #define PID_DUTY_CYCLE_MAX 1000 /* USER CODE END PD */
Как видите, реализация довольно проста и логична, но основная сложность при использовании ПИД-регулятора кроется в его настройке, чем мы и займемся в следующей статье.
Тоже годная статья на EE - ссылка.
Ссылка на проект - MT_PID_Project.












Правильно ли я понимаю, что интегральная составляющая остановится на каком-то одном значении и будет колебаться возле нее?
И еще, при вычислении производной, в первый раз что брать в качестве предыдущей невязки?
Можно считать, что дифф. составляющая будет равна нулю на первом шаге и станет вносить вклад только когда температура начнет изменяться за счет действия пропорциональной составляющей.
А по поводу интегральной - да, когда температура достигнет той величины, которая нам необходима, интегральная составляющая перестанет изменяться.
Понял, спасибо.
всегда интересовасля пид-регуляторами. спасибо за пояснение
Спасибо большое за эти статьи. Как раз возникла аналогичная задача. Имеются два двигателя от шуруповёртов и датчики количества оборотов и необходимо, чтобы они производили одинаковое количество оборотов всегда, ну или пропорционально один больше другого на определённое количество. Начал сам придумывать как это реализовать. Додумался до пропорциональной и дифференциальной составляющей, но чувствовал, что чего-то не хватает. Ваша статья всё прояснила - оказывается всё давным давно придумано. Ещё раз спасибо!
CMSIS-DSP Verison 1.1.0
CMSIS DSP Software Library
Там есть ВСЁ
Классно изложили суть всех составляющих объяснив как они себя ведут в процессе, это самое ценное. Спасибо
Cпасибо Вам большое!
Не за что ) Очень хорошо, если статья полезной оказалась )
Статья очень понравилась.В данное время будем применять ТРМ вместо автотрансформаторов для регулирования температуры в 3 зонной электрической печи.И вот какие коэффиценты при ПИД регулировании установить нужно.
С уважением Виталий.
спасибо, написал курсач за 5 минут
Супер =)
"Дифференциальная составляющая вносит свой вклад в мощность и представляет из себя производную температуры, взятую также с определенным коэффициентом (в программе для контроллера необходимо брать разницу между текущим значением невязки и предыдущим)."
Производная температуры это не разница между текущим значением невязки и предыдущим. Это наверно описка. Спасибо.
Спасибо!
Всетаки наверное это разница между текущим и вредыдущем значениями отклонения измеряемого сигнала помноженного на дифференциальный коэфfициент. Kd*(e(n) - e(n - 1)) = Kd*e(n) - Kd*e(n-1)
Только нужно еще учесть интервал времени, за который произошло это изменение.
ОТ души ребята, чётко и понятно)) классная статья!
Спасибо за отличный отзыв! =)
Первая из около 10 ти статей, где написано доходчиво как работает PID регулятор. спасибо
Спасибо! Рад, что понравилось!
а зачем в конце главного цикла обнуляется счётчик миллисекунд (timeCounterMs = 0;) ? Тогда ведь в начале следующего цикла счётчик секунд будет всегда 0
В начале цикла - да, потом выполнятся команды для датчика, и в счетчике как раз будет текущее значение, которое нужно в расчетах использовать.
спасибо за ответ!
Я правильно понимаю, что если у нас регулятор температуры и воздействует нагреватель, то (ошибка = целевое значение - текущее), а если воздействует охладитель, то наоборот (ошибка = текущее значение - целевое)? Либо коэффициенты должны быть в одном случае положительными, в другом отрицательными.
Иначе для нагревателя вот эта строка
даст отрицательное значение, Kp >0 на него умножится, и в итоге ШИМ установится в минимальное значение 0, и нагрева вообще не произойдёт
Код рабочий. Но приведенный код больше заготовка.
На днях импортировал на Си "PID basic functions "CONT_C", которую Сименс встраивает в свои PLC (теперь она крутится на STM32). Математика элементарная, всё по канонам. Но что понравилось в их реализации, и чего не смог найти "в интернете":
Очень заинтересовал Ваш комментарий насчет импорта кода из Сименса.
Я ломаю голову как доработать написанный мной для ряда задач ПИ-регулятор.
Понял, что надо улучшить.
И в части отключения накопления интегр.составляющей.
И в части безударного включения в Автомат.
А время, как назло, уже поджимает.
Понимаю, что некрасиво просить поделиться результатами Вашего труда (импорта).
Я готов сам посидеть, помозговать и импортировать себе в код что-то.
Но просто не соображу пока где искать эти исходники Сименса.
Помогите, пожалуйста, чем можете.
Может какие-то фрагменты их исходника. Или ссылки какие-то.
Заранее очень благодарен!
Уже давно портировал на С "Continuous Control" FB41 (CONT_C). Крутится на STM32, проблем нет. Но в CONT_C нет автотюна.
Автотюн есть в "Continuous Temperature Controller" FB58 (TCONT_CP). Снял защиту, транслировал STL ("ассемблерный" код Сименса) в SCL (паскалеподобный язык). Проверил SCL на реальном S7-1200 - работает.
С FB58 возился ради автотюнинга, но не понравился алгоритм и результат автотюна. На этом же стенде, автотюн более новой библиотеки PID_Compact от S7-1200/1500 даёт лучший результат. Из-за этого портировать FB58 на С/С++ не буду.
Итого выложил на гугле диске 2 папки: работающий С код FB41. И FB58 (переименованная в FB60) в исходниках на SCL. Ссылка
Сергей, всё скачал, открыл. Буду вникать и пробовать.
Огромное спасибо и за подробные пояснения, и за сами файлы!
Желаю успехов во всех делах!!!
Добрый день, есть пара вопросов по поводу настройки ПИД регулятора, можно попросить у вас с этим помощи ?
Да можно конечно, по мере возможности и наличия времени постараюсь подсказать.
Написал вот такой пид регулятор, timeCountMs изменяется по таймеру, не понимаю как правильно получать текущую скорость вращения мотора, как ее правильно определить ? (скорость это количество оборотов за условную единицу времени)
все вызовы функций корректны, ошибок компиляции не возникает.
Задача состоит в том чтобы менять скорость вращения от 0..100%
максимальная частота ШИМ 2кГц
Какая-то обратная связь есть, чтобы реальную скорость вращения получить (датчик итп)?
имеется только энкодер, подключенный к валу мотора
А, ну и он заведен на TIM8 видимо? А что именно не работает? Можно разбить на части - верно ли измеряется текущая скорость, верно ли рассчитывается dutyCyclePWM итд.
скорость вращения зависит от dutyCyclePWM, но измерение currSpeed это почему-то не текущая скорость, как раз проблема в том что не получается корректно рассчитать скорость
Надо targetSpeed и currSpeed чтобы были в одинаковых единицах измерения. Сейчас какие вообще порядки значений на практике имеются?
targetSleed скорость в оборотах значения может изменяться в пределах от 0 до 300
currentSpeed изменяется от 0 до 450, нооо....
currentSpeed показывает не скорость вращения, а общее количество оборотов мотора
Надо за какое-то время считать кол-во оборотов и высчитывать скорость вращения получается.
currSpeed = (float)TIM8->CNT / (N * 60);
что-то вроде этого?
Там в CNT - кол-во импульсов энкодера, а в N - кол-во импульсов на оборот?
Тогда если раз в секунду выполнять расчет, то TIM8->CNT / N - кол-во оборотов в секунду, (TIM8->CNT / N) * 60 - об / мин.
все верно,
завтра попробую, отпишусь что как, заранее спасибо
Окей, главное не забыть этот расчет проводить через равные промежутки времени, либо время с предыдущего расчета учесть в самой формуле, ну и соответственно кол-во оборотов чтобы было именно за этот период.
нет ли случаем примера, как учитывать время расчета, программа в данный момент не работает
https://disk.yandex.ru/d/ZpkQg_9jfJuraQ
ссылка на проект
Примерно так должно быть (псевдокод):
uint32_t timeStamp = 0; void main() { timeStamp = HAL_GetTick(); while(1) { HAL_Delay(600); uint32_t timeElapsed = HAL_GetTick() - timeStamp; timeStamp = HAL_GetTick(); uint32_t encoderCounts = TIM8->CNT; float revsPerElapsedTime = (float)encoderCounts / (float)N; float revsPerSecond = 1000 / (float)timeElapsed * revsPerElapsedTime; float revsPerMinute = revsPerSecond * 60; // PID process // ... } }Соответственно, тут банальный Delay(), в реальности, как вариант, по таймеру обработка.