Всем доброго времени суток! В сегодняшней статье будут ознакомительные процессы с темой искусственных нейронных сетей. Если взять всю мою деятельность, то вышеупомянутая тематика, пожалуй, вызывает у меня наибольший интерес, так что соответствующая рубрика на нашем сайте будет активно дополняться, расширяться и развиваться. Причем как за счет теоретических материалов, так и за счет реальных практических примеров с реализацией решения тех или иных задач. Итак, на этом краткую вводную часть завершаем и переходим к сути вопроса.
В этой статье, в первую очередь, проведем обзор ключевых терминов и нюансов, связанных с устройством и функционированием нейронных сетей. Далее же очевидным и логичным шагом будет перейти к процессу обучения, чему и будет посвящен следующий пост, но пока не забегаем вперед.
Итак, пойдем четко по выстроенному плану, дабы изложение материала было максимально структурированным и понятным 👌
Введение в искусственные нейронные сети.
Нейронная сеть представляет из себя математическую модель, построенную по образу и подобию реальных биологических нейронных систем. Под этими биологическими системами, в первую очередь, подразумеваются сети, состоящие из нервных клеток живых организмов. Изначальной мотивацией для появления нейронных сетей являлось желание смоделировать процессы, происходящие в мозге при помощи некоторого математически-алгоритмического инструмента. На нынешний момент искусственные нейронные сети более чем успешно применяются для целого ряда задач, среди которых можно выделить большие группы по виду деятельности:
- прогнозирование
- распознавание образов
- анализ данных
- запоминание информации
- классификация
- сжатие данных
И спектр возможных применений постоянно, неизбежно и очень стремительно растет.
Нейрон.
Что же из себя представляет искусственная нейронная сеть? В данном случае ответ уже следует из названия - сеть представляет из себя совокупность нейронов, соединенных друг с другом определенным образом. Рассмотрим один нейрон...
Нейрон представляет из себя элемент, который в соответствии с определенным правилом вычисляет значение выходного сигнала из входного. На практике обычно на вход конкретного нейрона поступают сигналы с нескольких других, аналогично же и с выхода сигнал идет также на некоторое количество элементов. Из взаимодействий данного вида и складывается результирующая нейронная сеть. По итогу мы получаем следующее:
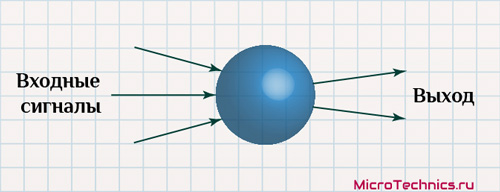
Таким образом, последовательность действий, выполняемых отдельно взятым нейроном, может быть представлена в виде четкой последовательности шагов:
- Прием сигналов от предыдущих элементов сети.
- Вычисление выходного сигнала.
- Передача этого рассчитанного сигнала далее по назначению.
Между собой нейроны могут быть соединены абсолютно по-разному, это определяется структурой конкретной сети. Но суть работы остается всегда одной и той же. По совокупности поступающих на вход сети сигналов формируется выходной сигнал. То есть нейронную сеть упрощенно можно представить в виде черного ящика, у которого есть входы и выходы. А внутри этого ящика находится некое количество нейронов.
Выделив в виде отдельных этапов протекающие в нейронной сети процессы, теперь закономерно перейдем к отдельному рассмотрению каждого из них в отдельности.
Комбинирование входных сигналов.
Поскольку к каждому нейрону могут приходить несколько входных сигналов, то при моделировании нейронной сети необходимо задать определенный механизм для комбинирования всех этих сигналов. То есть, по сути, нужно правило, как из приходящих сигналов получить конкретное значение, из которого будет рассчитан выходной сигнал нейрона. И для решения этой задачи часто используется правило суммирования взвешенных значений. Сейчас детально разберемся, что это означает на практике.
Рассмотрим связь между двумя элементами нейронной сети:
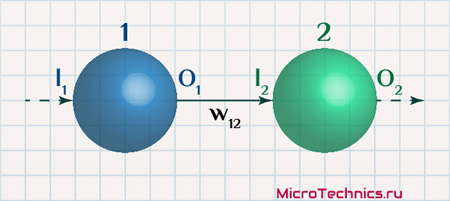
Каждую связь можно полностью охарактеризовать при помощи трех "параметров":
- первый - элемент, от которого исходит связь
- второй - элемент, к которому связь направлена
- третий - вес связи
Связи между нейронами так же называются синапсами, каждый из которых имеет свой вес. И именно вес синапса определяет, как выходной сигнал одного нейрона интерпретируется на входе другого нейрона. В данном примере имеем:
- O_1 – выходной сигнал нейрона 1
- w_{12} – вес синапса между нейронами 1 и 2
- I_2 – значение на входе нейрона 2
И связаны эти параметры в данном случае будут так:
I_2 = O_1 \cdot w_{12}То есть весь связи определяет, будет ли сигнал нейрона ослаблен (w_{12} < 1) или усилен (w_{12} >1) в результате прохождения через эту связь. Расширим наш пример:
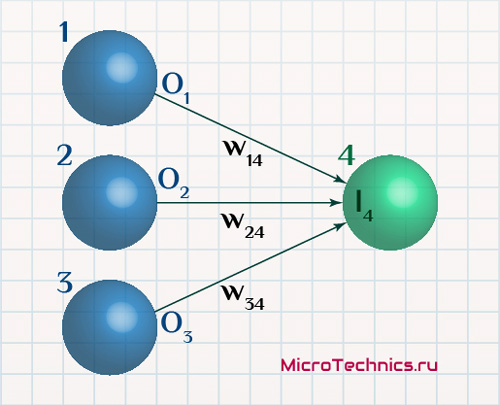
Здесь картина меняется – нейрон 4 связан с целым рядом «предшествующих» ему нейронов сети. Но алгоритм расчета неизменен:
I_4 = O_1 \cdot w_{14} + O_2 \cdot w_{24} + O_3 \cdot w_{34}Что в общем виде становится:
I_j = \sum_{i=1}^{N}{O_i\medspace w_{ij}}Присутствуют следующие действующие лица:
- I_j - это результат комбинирования всех входных сигналов для нейрона j (комбинированный ввод нейрона)
- N - количество элементов, передающих свои выходные сигналы на вход нейрона j
- w_{ij} - вес связи, соединяющей нейрон i с нейроном j
Мы для наглядности обозначили входы и выходы - I_j (Input) и O_i (Output) - но везде может быть своя система наименований. Например, комбинированный ввод часто обозначается как net_j. На принципах работы это в любом случае никак не отражается, просто имейте ввиду.
Алгебраически суммируя все взвешенные входные сигналы, мы получаем комбинированный ввод элемента сети. Для наглядности, конечно же, практический пример:
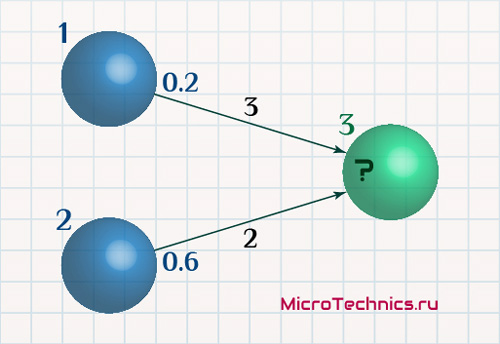
Определяем комбинированный ввод нейрона 3:
I_3 = O_1 \cdot w_{13} + O_2 \cdot w_{23} = 0.2 \cdot 3 + 0.6 \cdot 2 = 1.8Все, дело сделано. С весовыми коэффициентами и комбинированным вводом разобрались, двигаемся дальше.
Структура искусственных нейронных сетей.
Нейроны в сети могут быть взаимосвязаны и расположены друг относительно друга абсолютно по-разному. Это зависит от решаемой задачи – так, например, для задачи кластеризации отлично подходит нейронная сеть Кохонена, соответственно, структура конкретной сети для конкретной задачи будет продиктована, в первую очередь, типом нейронной сети. Мы сегодня будем рассматривать в основном сети прямого распространения, в которых сигналы двигаются строго от входных элементов к выходным. При этом наличествовать могут также и скрытые слои:
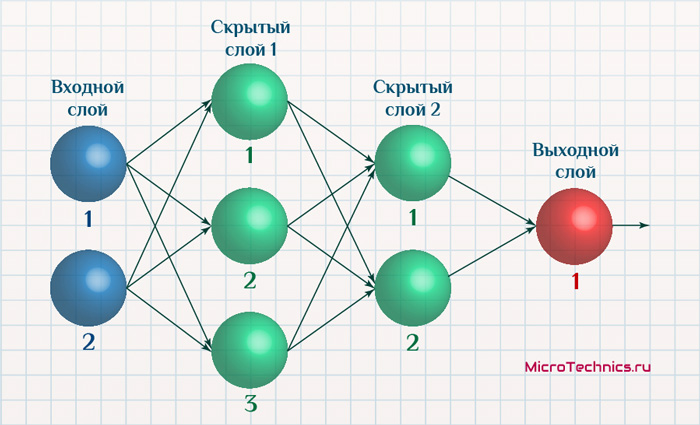
- входной слой (нейроны входного слоя)
- скрытый слой 1
- скрытый слой 2
- выходной слой
Чаще всего структура связей между нейронами представляется в виде матрицы W, которую называют весовой матрицей. Элемент матрицы w_{ij} (i-я строка, j-й столбец) определяет вес связи, идущей от элемента j слоя к элементу i следующего. Для того, чтобы понять, как составляются весовые матрицы, давайте установим значения весов для этой сети:
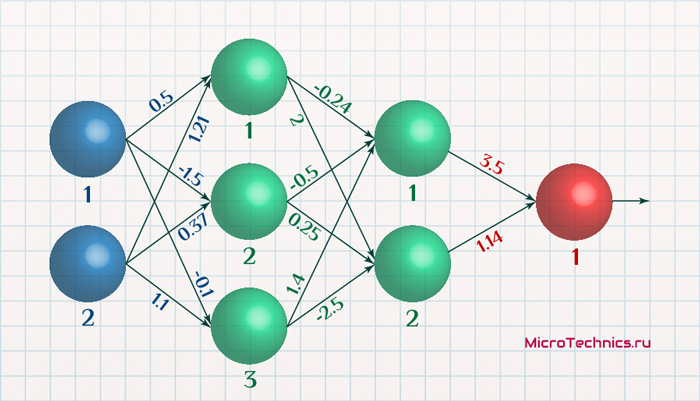
И записываем весовую матрицу для связей между входным и первым скрытым слоем:
W = \begin{vmatrix} w_{11} & w_{12} \hspace{0.6em}\\ w_{21} & w_{22} \hspace{0.6em}\\ w_{31} & w_{32} \hspace{0.6em}\\ \end{vmatrix} = \begin{vmatrix} 0.5 & 1.21 \hspace{0.6em}\\ -1.5 & 0.37 \hspace{0.6em}\\ -0.1 & 1.1 \hspace{0.6em}\\ \end{vmatrix}Например, от второго элемента входного слоя к третьему скрытого идет связь, вес которой равен 1.1. Смотрим на матрицу, второй столбец, третья строка - число 1.1, соответствует значению веса связи. Аналогичным образом составляется матрица, например, для связей между первым и вторым скрытыми слоями:
W = \begin{vmatrix} w_{11} & w_{12} & w_{13} \hspace{0.6em}\\ w_{21} & w_{22} & w_{23} \hspace{0.6em}\\ \end{vmatrix} = \begin{vmatrix} -0.24 & -0.5 & 1.4 \hspace{0.6em}\\ 2 & 0.25 & -2.5 \hspace{0.6em}\\ \end{vmatrix}Конфигурация сети зависит от условий ее использования, то есть от той задачи, которую данная сеть призвана решать. Помимо вышеописанного сеть может иметь в своем составе так называемые нейроны смещения:
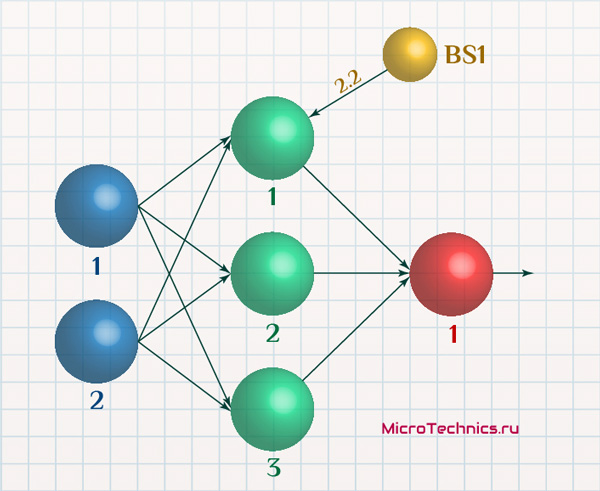
Здесь элемент с номером BS1 - нейрон смещения.
Отличительной и ключевой особенностью нейрона смещения является тот факт, что его выходной сигнал всегда равен единице. В завершающем разделе статьи рассмотрим реальный пример нейронной сети, в том числе содержащей и нейроны смещения, так что на практике развеем неясные моменты, если они имеются.
Функция активации нейрона.
Входные сигналы и структуру мы рассмотрели, пришло время выходных. Для каждого элемента нейронной сети имеется определенное правило, в соответствии с которым из значения комбинированного ввода вычисляется выходное значение. И правило это называется функцией активации. Для нейронов входного слоя есть исключение - на их выходе имеем то же самое, что и на входе.
В роли функции активации может выступать достаточно большое количество различных функций, пройдемся немного по некоторым из вариантов. А в будущем, по мере расширения курса, на реальных задачах посмотрим, когда и что является менее или более применимым.
Небольшое лирическое отступление. При работе с реальными нейронными сетями зачастую нет конкретных и единственно верных ответов на возникающие в процессе вопросы – «сколько сделать слоев?», «сколько нейронов должно быть в каждом слое?», «какая функция активации должна использоваться?». Завеса тайны приоткрывается исключительно в ходе экспериментов и исследования поведения той или иной сети. Параметры, дающие результат для одной задачи, с вероятностью, близкой к 100%, не будут работать аналогично для задачи другого рода и т. п. Поэтому разработка решения на базе искусственной нейронной сети в большинстве случаев – это не просто точное следование определенным шагам, это в некотором роде творческий процесс 👍
Итак, несколько примеров функций активации.
- Сигмоидальная функция, она же сигмоида:
f(x) = \frac{1}{1 + e^{-x}}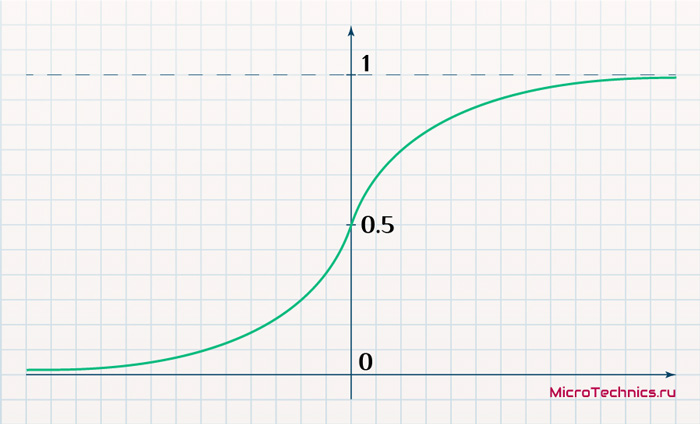
- Гиперболический тангенс:
f(x) = tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}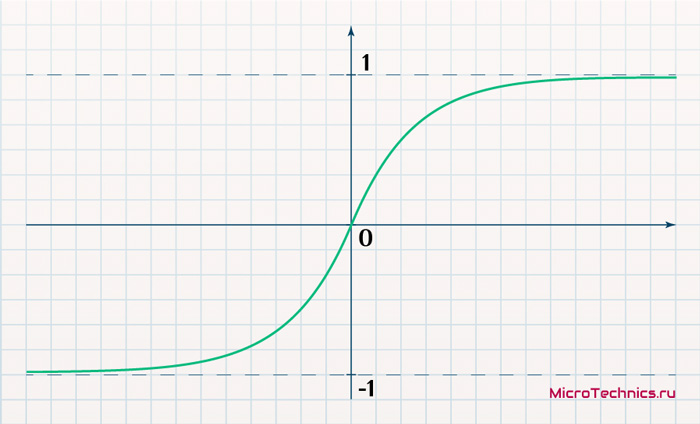
- ELU (Exponential Linear Units):
f(x) = \begin{cases}
x &\text {если } x \ge 0 \\
\alpha(e^x - 1) &\text {если } x < 0
\end{cases}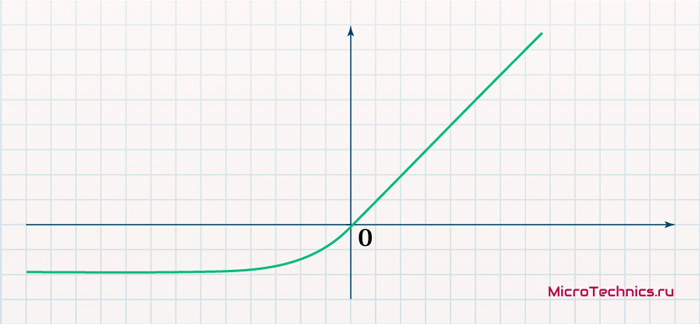
Более подробно не буду расписывать все варианты, лучше рассмотрим в отдельной статье, исключительно о функциях активации нейронов. А пока, как вариант, вот тут можно найти информацию.
Соответственно, используемая функция определяет диапазон, в котором может изменяться выходной сигнал нейрона. В частности, для сигмоидальной функции активации выходное значение всегда от 0 до 1, каким бы не было значение на входе.
Работа функции активации, таким образом, заключается в следующем:
O_i =f(I_i)
То есть в вычислении из значения комбинированного ввода элемента его выходного сигнала, который отправится к следующим нейронам сети (для нейрона скрытого слоя), либо прямиком на выход сети (для нейрона выходного слоя).
Тем временем мы добрались для логического завершения, а именно до демонстрации всего описанного на реальном практическом примере.
Пример решения задачи XOR с помощью нейронной сети.
При изучении языков программирования классическим примером является “Hello world”, для микроконтроллеров – моргание диодом, есть аналогичный по своей сути пример и для нейронных сетей. И заключается он в использовании нейронной сети для вычисления результата выполнения логической операции XOR (исключающее ИЛИ). Таблица истинности выглядит так:
| x | y | x XOR y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
На вход сети мы будем подавать значения из первых двух столбцов, а на выходе должны получить значение из третьего. Соответственно, сама постановка задачи диктует нам условия в плане структуры сети. Очевидно, что входных нейронов должно быть два, а выходной – один. Поскольку механизмы бучение нейронных сетей мы пока не рассматривали, то возьмем уже обученную сеть и произведем для нее расчеты, аналогичные тем, которые мы обсуждали на протяжении всей статьи:

В качестве функции активации будет выступать пороговая функция:
f(x) = \begin{cases}
1 &\text {если } x \ge 0 \\
0 &\text {если } x < 0
\end{cases}Подаем на вход сети значения 0 и 0 и рассчитываем значение на выходе сети для данных входных образцов:
- Входной слой: O_1 = I_1 = 0, O_2 = I_2 = 0.
- Входные сигналы скрытого слоя 1: I_3 = 0 \cdot (-1) + 0 \cdot (-1) + 1.5 = 1.5, I_4 = 0 \cdot (-1) + 0 \cdot (-1) + 0.5 = 0.5. Обратите внимание на нейроны смещения.
- Выходные сигналы скрытого слоя 1: O_3 = f(1.5) = 1, O_4 = f(0.5) = 1.
- Входной сигнал выходного слоя: I_7 = 1 \cdot 1 + 1 \cdot (-1) + (-0.5) = -0.5
- Выход сети: O_7 = f(-0.5) = 0
Как видите, полученное значение в точности соответствует значению в третьем столбце таблицы истинности. Продолжаем расчеты для второй строки, то есть на вход подаем 0 и 1:
- O_1 = I_1 = 0, O_2 = I_2 = 1.
- I_3 = 0 \cdot (-1) + 1 \cdot (-1) + 1.5 = 0.5, I_4 = 0 \cdot (-1) + 1 \cdot (-1) + 0.5 = -0.5.
- O_3 = f(0.5) = 1, O_4 = f(-0.5) = 0.
- I_7 = 1 \cdot 1 + 0 \cdot (-1) + (-0.5) = 0.5
- O_7 = f(0.5) = 1
И снова результат закономерен и ожидаем. Если продолжить, то для всех возможных комбинаций значений сигналов на входе получим выходной сигнал, соответствующий требуемому. А значит сеть успешно справляется с задачей вычисления результата операции XOR.
И на этом на сегодня мы заканчиваем с искусственными нейронными сетями, спасибо за внимание и не пропускайте новые материалы на нашем сайте 🤝












Не понял откуда в примере появились значения -1 ведь f(x) больше или равна 0 при любых x.
Весовые коэффициенты.
Спасибо.
Статья интересная. Спасибо. Только поправьте пожалуйста вот здесь : "Аналогичным образом составляется матрица, например, для связей между вторым скрытым и выходным слоем:" ибо матрицу вы приводите для связей между первым скрытым и вторым скрытым слоем....
Благодарю!