Продолжаем обсуждение катушек индуктивности, в первой части (ссылка) мы обсудили все основные аспекты, а именно устройство катушек, принцип работы и их поведение при использовании в цепях постоянного и переменного тока. Но некоторые моменты остались незатронутыми, собственно, их мы и обсудим в этой статье. И начнем с очень важной характеристики, а именно добротности катушки индуктивности.
Активное сопротивление и добротность катушки индуктивности.
Итак, начнем мы с того, что обсудим некоторые характеристики катушек индуктивности, с которыми мы не успели познакомиться в предыдущей статье. И для начала рассмотрим активное сопротивление катушки.
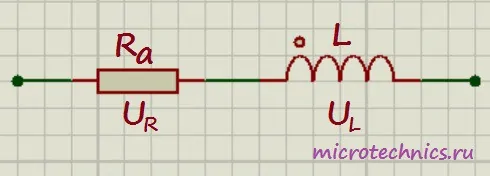
Разбирая примеры включения катушек в различные цепи, мы считали их активное сопротивление равным 0 (такие катушки называют идеальными). Но на практике любая катушка обладает ненулевым активным сопротивлением. Таким образом реальную катушку индуктивности можно представить как идеальную катушку и последовательно включенный резистор:
Идеальная катушка, как вы помните, не оказывает никакого сопротивления постоянному току, и напряжение на ней равно 0. В случае с реальной катушкой ситуация несколько меняется. При протекании по цепи постоянного тока напряжение на катушке будет равно:
U_L = IR_а
Ну а поскольку частота тока равна 0 (постоянный ток), то реактивное сопротивление:
X_L = 2\pi f L = 0
А что же будет происходить при включении реальной катушки индуктивности в цепь переменного тока? Давайте разбираться. Представим, что по данной цепи течет переменный ток i, тогда общее напряжение на цепи будет складываться из следующих компонент:
u = iR + u_L
Напряжение на идеальной катушке, как вы помните, выражается через ЭДС самоиндукции:
u_L = -\varepsilon_L = L\frac{di}{dt}И мы получаем для напряжения на реальной катушке индуктивности:
u = iR + L\frac{di}{dt}Отношение реактивного (индуктивного) сопротивления к активному называется добротностью и обозначается буквой Q:
Q = \frac{X_L}{R}Раз активное сопротивление R идеальной катушки равно 0, то значит ее добротность Q будет бесконечно большой. Соответственно, чем выше добротность катушки индуктивности, тем она ближе к идеальной. Таким образом активное сопротивление катушки мы рассмотрели, перейдем к следующему вопросу.
Энергия катушки индуктивности.
Электрический ток, протекающий через катушку способствует накоплению энергии в магнитном поле катушки. При пропадании/отключении тока эта энергия будет возвращена в электрическую цепь. С этим мы и столкнулись при рассмотрении катушек индуктивности в цепях постоянного тока. Больше тут добавить особо нечего, просто приведу формулу, по которой можно определить величину этой накопленной энергии:
W = \frac{LI^2}{2}Планомерно переходим к вариантам соединения катушек между собой. Все расчеты будем производить для идеальных катушек индуктивности, то есть их активные сопротивления равны 0. К слову, в большинстве теоретических задач и примеров, рассматриваются именно идеальные катушки. Но не стоит забывать о том, что в реальных цепях активное сопротивление не равно 0, и его необходимо учитывать при проведении любых расчетов.
Последовательное соединение катушек индуктивности.
При последовательном соединении катушек индуктивности их можно заменить одной катушкой с величиной индуктивности, равной:
L_0 = L_1 + L_2
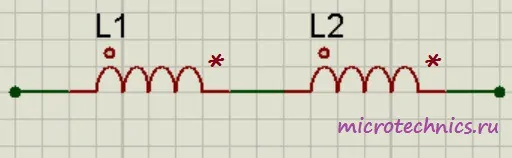
Вроде все просто, но тут есть один немаловажный нюанс. Данная формула справедлива только в том случае, если катушки расположены на таком расстоянии друг от друга, что магнитное поле одной катушки не пересекает витков другой:
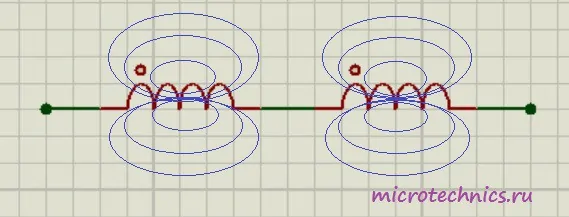
Если же катушки расположены близко друг к другу и часть магнитного поля одной катушки пронизывает вторую, то тут ситуация несколько другая. Возможны два варианта:
- магнитные потоки катушек имеют одинаковое направление
- магнитные потоки направлены навстречу друг другу
Первый случай называется согласным включением катушек - начало второй катушки подключается к концу первой. А второй вариант называют встречным включением - конец второй катушки подключается к началу первой. На схемах начало катушки обозначают символом "*". Таким образом, на схеме, которая представлена на рисунке мы имеем согласное включение катушек индуктивности. Для этого случая общая индуктивность определяется так:
L = L_1 + L_2 + 2M
Где M - взаимная индуктивность катушек. При встречном включении последовательно соединенных катушек индуктивности:
L = L_1 + L_2\medspace-\medspace 2M
Можно заметить, что если потоки имеют одинаковое направление (согласное включение), то общая индуктивность увеличивается на двойную величину взаимной индуктивности. А если потоки направлены навстречу друг другу - уменьшается на ту же самую величину.
Параллельное соединение катушек индуктивности.
При параллельном соединении катушек индуктивности также возможны три варианта:
- Магнитное поле одной катушки не пересекает витков второй катушки, тогда: \frac{1}{L_0} = \frac{1}{L_1} +\frac{1}{L_2} или L_0 = \frac{L_1L_2}{L_1 + L_2}
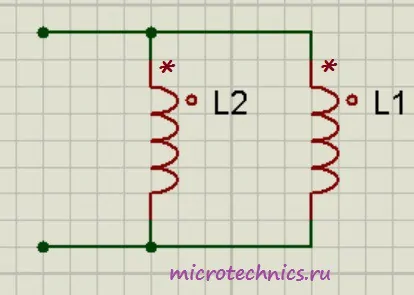
- Часть магнитного потока одной катушки пронизывает витки второй и катушки включены согласно (как изображено на рисунке - то есть начала обеих катушек подключены к одному узлу). В этом случае: L_0 = \frac{L_1L_2\medspace-\medspace M^2}{L_1 + L_2\medspace-\medspace 2M}
- Часть магнитного потока одной катушки пронизывает витки второй и катушки включены встречно. В этом случае: L_0 = \frac{L_1L_2\medspace-\medspace M^2}{L_1 + L_2 + 2M}
Также как и в случае с последовательным соединением, при согласном включении общая индуктивность будет больше, чем при встречном включении, поскольку знаменатель дроби будет меньше.
Собственно, на этом заканчиваем разбор катушек индуктивности. Ранее мы изучили конденсаторы и резисторы, а в будущих статьях нам предстоит работать с цепями, включающими все эти элементы. Так что подписывайтесь на обновления и не пропускайте новые статьи 🤝
