Всех приветствую, продолжаем изучать электронику с самых основ, и темой сегодняшней статьи будет катушка индуктивности. Забегая вперед скажу, что сначала мы обсудим теоретические аспекты, а несколько будущих статей посвятим целиком и полностью рассмотрению различных электрических схем, в которых используются катушки индуктивности, а также элементы, которые мы изучили ранее в рамках нашего курса - резисторы и конденсаторы.
Устройство и принцип работы катушки индуктивности.
Как уже понятно из названия элемента - катушка индуктивности, в первую очередь, представляет из себя не что иное, как катушку. То есть некоторое количество витков изолированного проводника. Причем наличие изоляции является важнейшим условием - витки катушки не должны замыкаться друг с другом. Чаще всего витки наматываются на цилиндрический или тороидальный каркас:
Важнейшей характеристикой катушки индуктивности является, естественно, индуктивность. По определению индуктивность - это способность преобразовывать энергию электрического поля в энергию магнитного поля. Это свойство катушки связано с тем, что при протекании по проводнику тока вокруг него возникает магнитное поле:
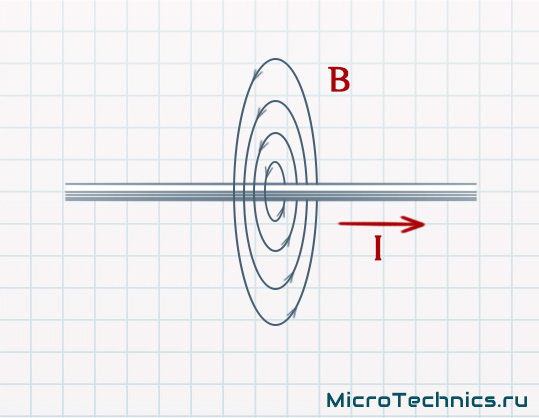
А вот как выглядит магнитное поле, возникающее при прохождении тока через катушку:
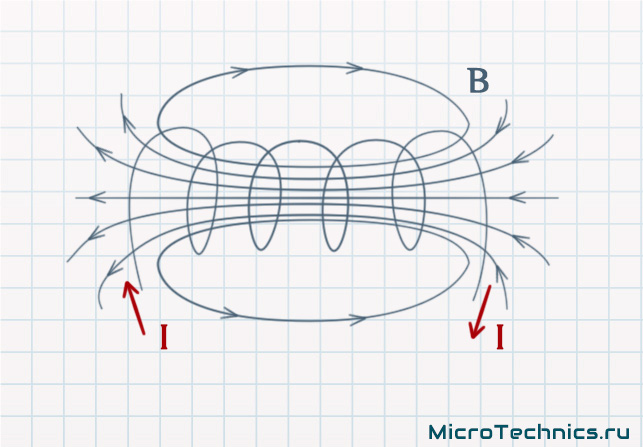
В общем то, строго говоря, любой элемент в электрической цепи имеет индуктивность, даже обычный кусок провода. Но дело в том, что величина такой индуктивности является очень незначительной, в отличие от индуктивности катушек. Собственно, для того, чтобы охарактеризовать эту величину используется единица измерения Генри (Гн). 1 Генри - это довольно большая величина, поэтому чаще всего используются мкГн (микрогенри) и мГн (миллигенри). Величину индуктивности можно рассчитать по следующей формуле:
L = \frac{\mu_0\thinspace \mu S N^2}{l}Разберемся, что за величины входят в это выражение:
- \mu_0 - магнитная проницаемость вакуума. Это константа и равна она: \mu_0 = 4 \pi \cdot 10^{-7}\medspace\frac{Гн}{м}
- \mu - магнитная проницаемость магнитного материала сердечника. Пара слов о том, что это за сердечник и для чего он нужен. Дело все в том, что если катушку намотать не просто на каркас (внутри которого воздух), а на магнитный сердечник, то индуктивность возрастет многократно. Посудите сами - магнитная проницаемость воздуха равна 1, а для никеля она может достигать величины 1100. Вот мы и получаем увеличение индуктивности более чем в 1000 раз
- S - площадь поперечного сечения катушки
- N - количество витков
- l - длина катушки
Из формулы следует, что при увеличении числа витков или, к примеру, диаметра (а соответственно и площади поперечного сечения), индуктивность будет увеличиваться. А при увеличении длины - уменьшаться. Таким образом, витки на катушке стоит располагать как можно ближе друг к другу, поскольку это приведет к уменьшению длины.
С устройством катушки индуктивности разобрались, пришло время рассмотреть физические процессы, которые протекают в этом элементе при прохождении электрического тока. Для этого мы рассмотрим две схемы - в одной будем пропускать через катушку постоянный ток, а в другой -переменный.
Катушка индуктивности в цепи постоянного тока.
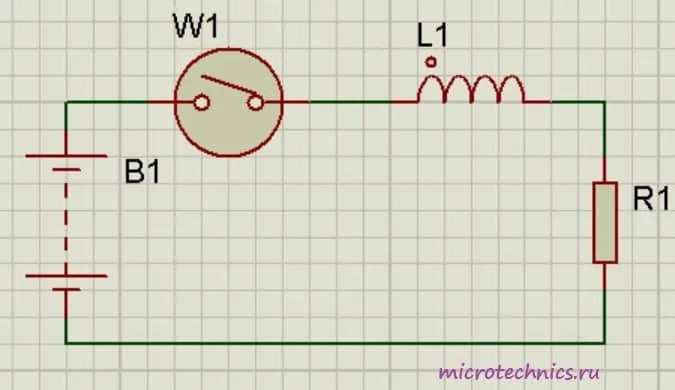
И, в первую очередь, разберемся, что происходит в самой катушке при протекании тока. Если ток не изменяет своей величины, то катушка не оказывает на него никакого влияния. Значит ли это, что в случае постоянного тока использование катушек индуктивности и рассматривать не стоит? Однозначно нет. Ведь постоянный ток можно "включать/выключать", и как раз в моменты переключения и происходят все ключевые процессы. Давайте рассмотрим цепь:
Резистор выполняет в данном случае роль нагрузки, на его месте могла бы быть, к примеру, лампа. Помимо резистора и индуктивности в цепь включены источник постоянного тока и переключатель, с помощью которого мы будем замыкать и размыкать цепь. Что же произойдет в тот момент когда мы замкнем выключатель?
Ток через катушку начнет изменяться, поскольку в предыдущий момент времени он был равен 0. Изменение тока приведет к изменению магнитного потока внутри катушки, что, в свою очередь, вызовет возникновение ЭДС (электродвижущей силы) самоиндукции, которую можно выразить следующим образом:
\varepsilon_s = -\frac{d\Phi}{dt}Возникновение ЭДС приведет к появлению индукционного тока в катушке, который будет протекать в направлении, противоположном направлению тока источника питания. Таким образом, ЭДС самоиндукции будет препятствовать протеканию тока через катушку (индукционный ток будет компенсировать ток цепи из-за того, что их направления противоположны). А это значит, что в начальный момент времени (непосредственно после замыкания выключателя) ток через катушку I_L будет равен 0. В этот момент времени ЭДС самоиндукции максимальна.
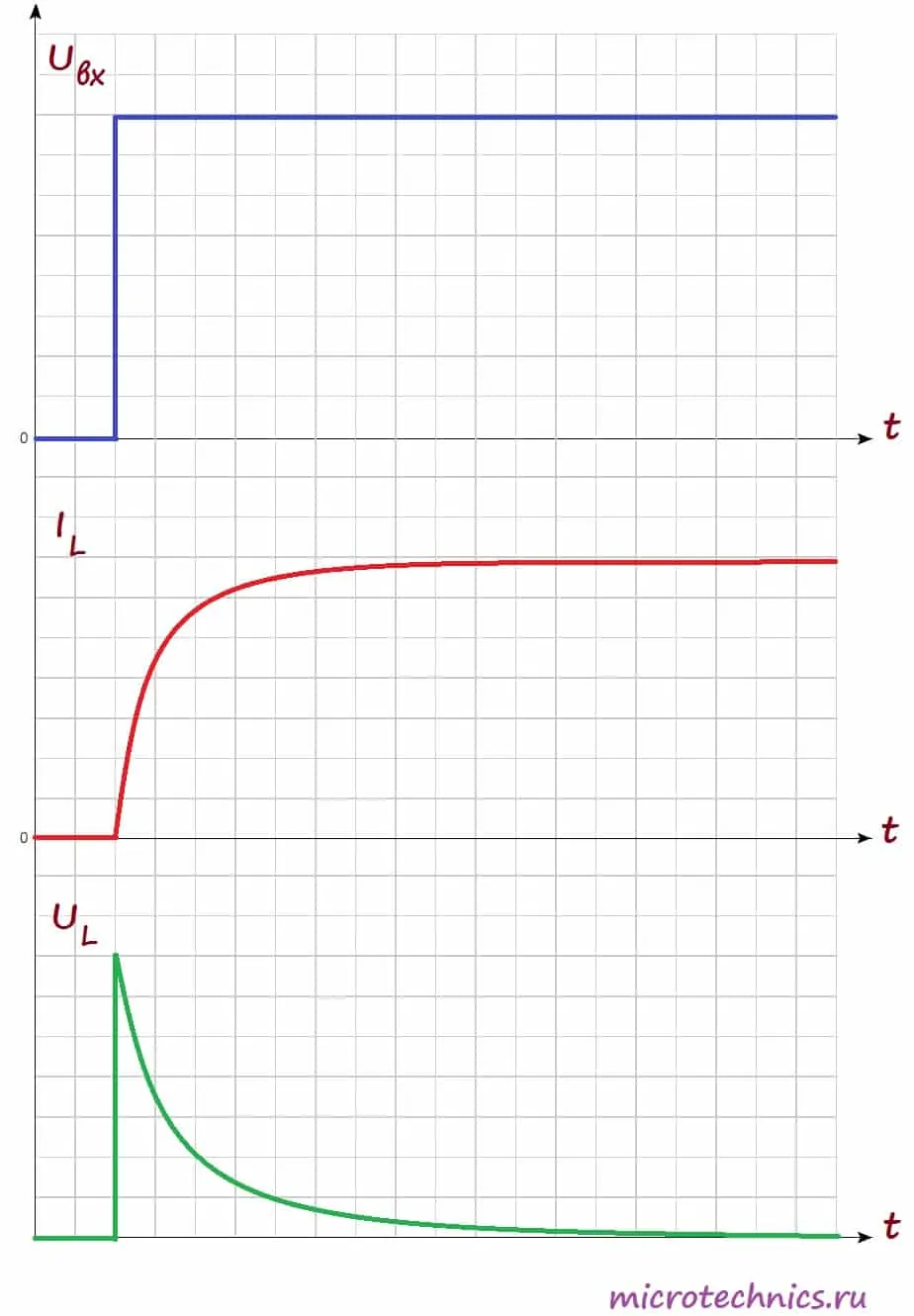
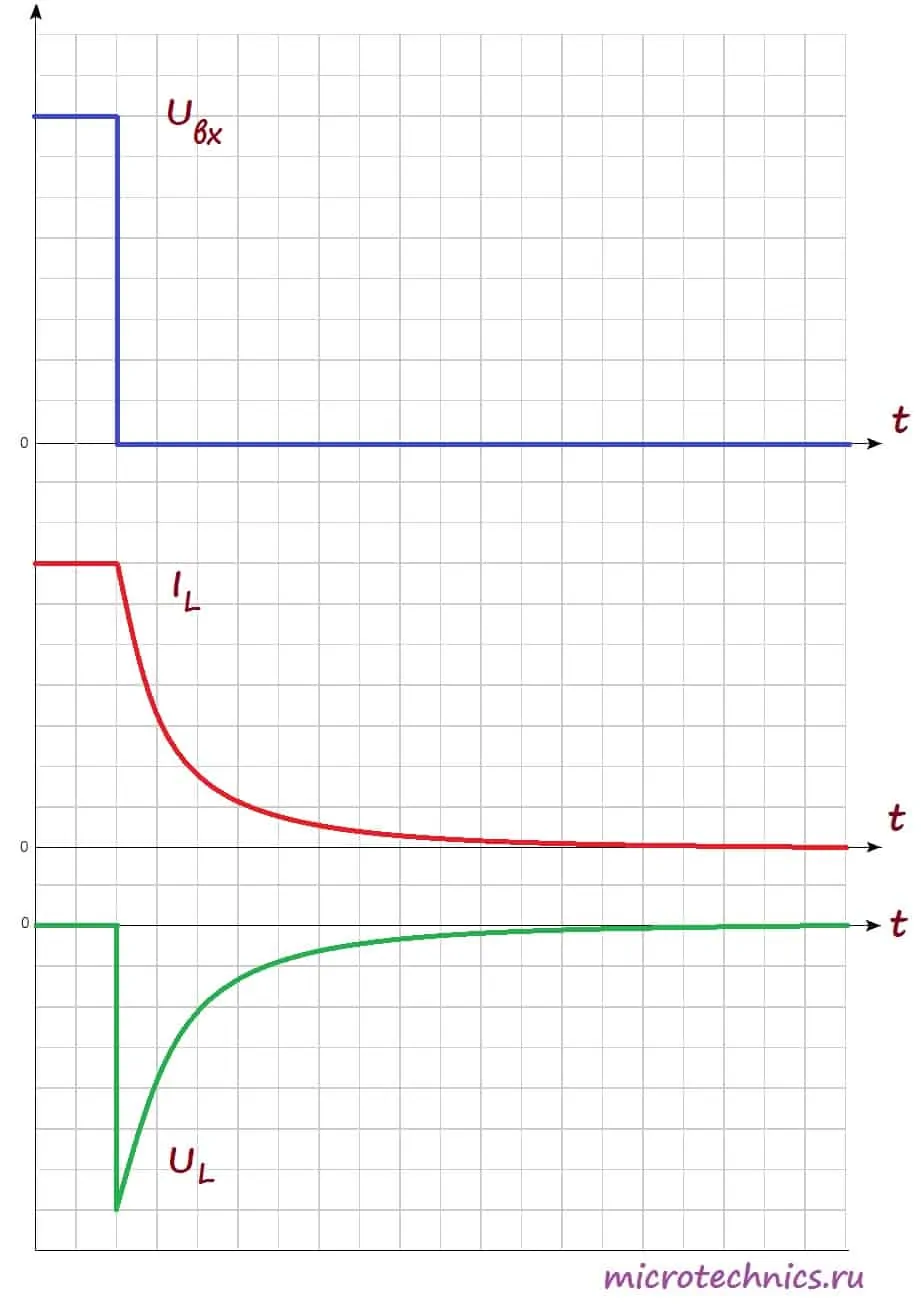
А далее произойдет следующее - поскольку величина ЭДС прямо пропорциональна скорости изменения тока, то она будет постепенно ослабевать, а ток, соответственно, наоборот, будет возрастать. Давайте посмотрим на графики, иллюстрирующие то, что мы обсудили:
На первом графике мы видим входное напряжение цепи - изначально цепь разомкнута, но при замыкании переключателя появляется постоянное значение. На втором графике мы видим изменение величины тока через катушку индуктивности. Непосредственно после замыкания ключа ток отсутствует из-за возникновения ЭДС самоиндукции, а затем начинает плавно возрастать.
Напряжение на катушке наоборот в начальный момент времени максимально, а затем уменьшается. График напряжения на нагрузке будет по форме (но не по величине) совпадать с графиком тока через катушку (поскольку при последовательном соединении ток, протекающий через разные элементы цепи одинаковый).
Аналогичный переходный процесс в цепи будет наблюдаться и при размыкании ключа. В катушке индуктивности возникнет ЭДС самоиндукции, но индукционный ток в случае размыкания будет направлен в том же самом направлении, что и ток в цепи, а не в противоположном, поэтому запасенная энергия катушки индуктивности пойдет на поддержание тока в цепи:
После размыкания ключа возникает ЭДС самоиндукции, которая препятствует уменьшению тока через катушку, поэтому ток достигает нулевого значения не сразу, а по истечении некоторого времени. Напряжение же в катушке по форме идентично случаю замыкания переключателя, но противоположно по знаку. Это связано с тем, что изменение тока, а соответственно и ЭДС самоиндукции, в первом и втором случаях противоположны по знаку (в первом случае ток возрастает, а во втором убывает).
Кстати, я упомянул, что величина ЭДС самоиндукции прямо пропорциональна скорости изменения силы тока, так вот, коэффициентом пропорциональности является как раз индуктивность катушки:
\varepsilon_s = -L\medspace\frac{dI}{dt}На этом мы заканчиваем с катушками индуктивности в цепях постоянного тока и переходим к цепям переменного тока.
Важный (!) нюанс заключается в том, что напряжение на катушке при описанных переходных процессах может достигнуть весьма значительных величин. Это, в свою очередь, легко может привести к выходу из строя тех или иных компонентов, входящих в состав цепи. Например, при управлении индуктивной нагрузкой при помощи ключа на транзисторе явление возникновения ЭДС самоиндукции с впечатляющей вероятностью приведет к выходу транзистора из строя. Для защиты от этого параллельно индуктивной нагрузке ставят защитный диод, но сегодня речь не об этом, поэтому для данного аспекта я опубликую отдельный материал с рассмотрением основных нюансов.
Катушка индуктивности в цепи переменного тока.
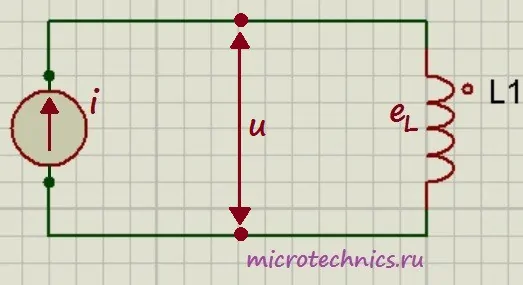
Рассмотрим цепь, в которой на катушку индуктивности подается переменный ток:
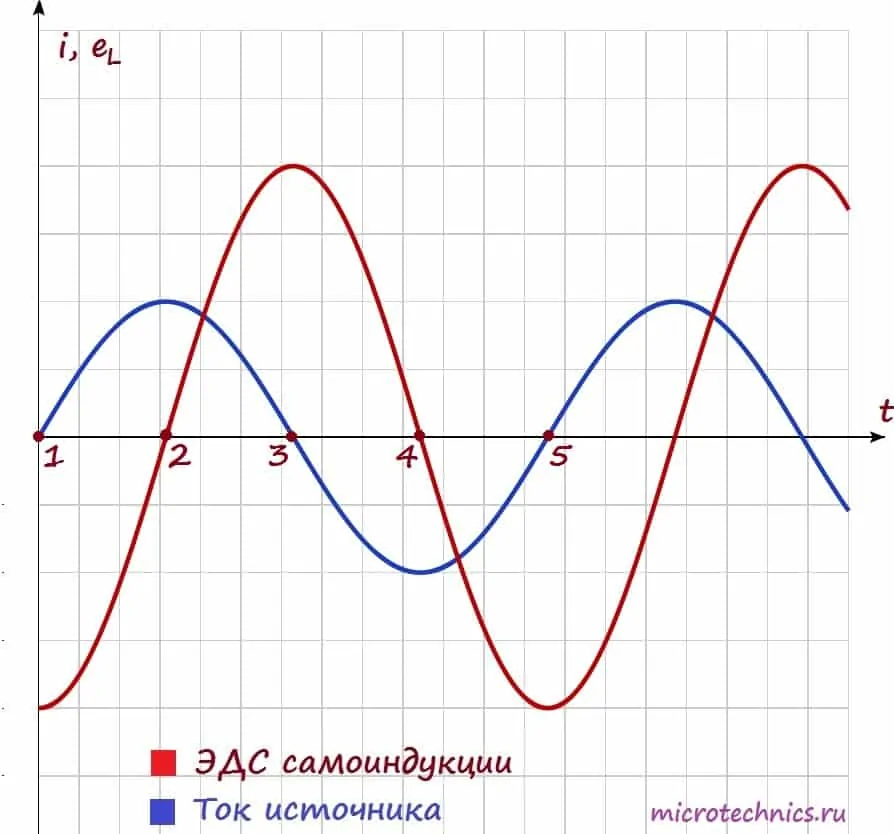
И теперь посмотрим на зависимости тока и ЭДС самоиндукции от времени, а затем уже разберемся, почему они выглядят именно так:
Как мы уже выяснили ЭДС самоиндукции у нас прямо пропорциональна и противоположна по знаку скорости изменения тока:
\varepsilon_L = -L\medspace\frac{dI}{dt}Собственно, график нам и демонстрирует эту зависимость. Смотрите сами - между точками 1 и 2 ток у нас изменяется, причем чем ближе к точке 2, тем изменения меньше, а в точке 2 в течение какого-то небольшого промежутка времени ток и вовсе не изменяет своего значения. Соответственно скорость изменения тока максимальна в точке 1 и плавно уменьшается при приближении к точке 2, а в точке 2 равна 0, что мы и видим на графике ЭДС самоиндукции. Причем на всем промежутке 1-2 ток возрастает, а значит скорость его изменения положительна, в связи с этим на ЭДС на всем этом промежутке напротив принимает отрицательные значения.
Аналогично между точками 2 и 3 - ток уменьшается - скорость изменения тока отрицательная и увеличивается - ЭДС самоиндукции увеличивается и положительна. Не буду расписывать остальные участки графика - там все процессы протекают по такому же принципу.
Кроме того, на графике можно заметить очень важный момент - при увеличении тока (участки 1-2 и 3-4) ЭДС самоиндукции и ток имеют разные знаки (участок 1-2: \varepsilon < 0, i > 0, участок 3-4: \varepsilon > 0, i < 0). Таким образом, ЭДС самоиндукции препятствует возрастанию тока (индукционные токи направлены "навстречу" току источника).
А на участках 2-3 и 4-5 все наоборот - ток убывает, а ЭДС препятствует убыванию тока (поскольку индукционные токи будут направлены в ту же сторону, что и ток источника и будут частично компенсировать уменьшение тока).
И в итоге мы приходим к очень интересному факту - катушка индуктивности оказывает сопротивление переменному току, протекающему по цепи. А значит она имеет сопротивление, которое называется индуктивным или реактивным, и вычисляется следующим образом:
X_L = w\medspace L
Где w - угловая частота: w = 2 \pi f. [/latex]f[/latex] - это частота переменного тока. Таким образом, чем больше частота тока, тем большее сопротивление будет ему оказывать катушка индуктивности. А если ток постоянный (f = 0), то реактивное сопротивление катушки равно 0, соответственно, она не оказывает влияния на протекающий ток.
Давайте вернемся к нашим графикам, которые мы построили для случая использования катушки индуктивности в цепи переменного тока. Мы определили ЭДС самоиндукции катушки, но каким же будет напряжение u? Здесь все просто, по 2-му закону Кирхгофа:
u + \varepsilon_L = 0
А следовательно:
u = - \varepsilon_L
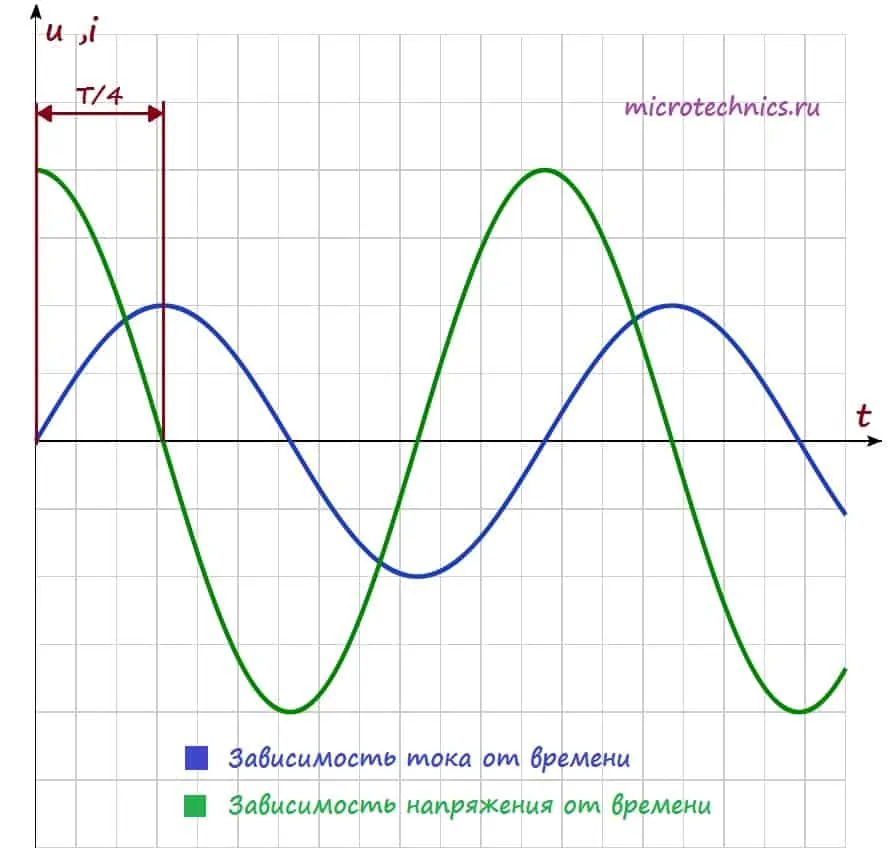
Построим на одном графике зависимости тока и напряжения в цепи от времени:
Как видите ток и напряжение сдвинуты по фазе (ссылка) друг относительно друга, и это является одним из важнейших свойств цепей переменного тока, в которых используется катушка индуктивности:
При включении катушки индуктивности в цепь переменного тока в цепи появляется сдвиг фаз между напряжением и током, при этом ток отстает по фазе от напряжения на четверть периода.
Вот и с включением катушки в цепь переменного тока мы разобрались 👍 На этом, пожалуй, закончим сегодняшнюю статью, она получилась уже довольно объемной, поэтому разговор о катушках индуктивности мы продолжим в следующий раз.
