Плоский конденсатор. Заряд и емкость конденсатора.

Наряду с резисторами одними из наиболее часто используемых электронных компонентов являются конденсаторы. И в этой статье мы разберемся, из чего они состоят, как работают и для чего применяются 👍 В первую очередь, рассмотрим устройство и принцип работы, а затем плавно перейдем к основным свойствам и характеристикам - заряду, энергии и, конечно же, емкости конденсатора.

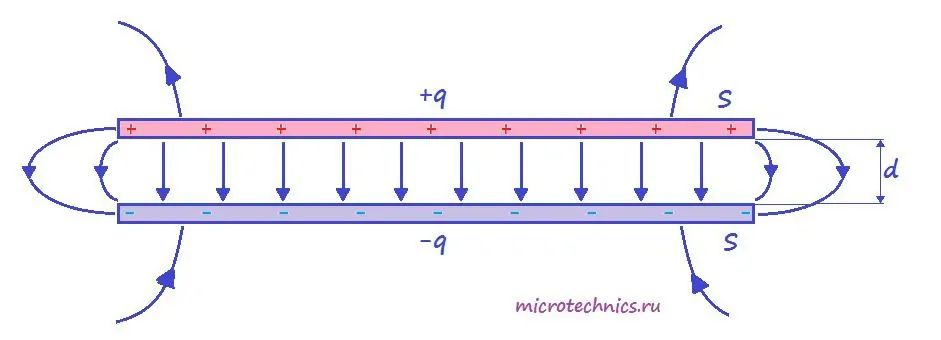
Плоский конденсатор.

Итак, простейший конденсатор представляет из себя две плоские проводящие пластины, расположенные параллельно друг другу и разделенные слоем диэлектрика. Причем расстояние между пластинами должно быть намного меньше, чем, собственно, размеры пластин:

Такое устройство называется плоским конденсатором, а пластины - обкладками конденсатора. Стоит уточнить, что здесь мы рассматриваем уже заряженный конденсатор (сам процесс зарядки мы изучим чуть позже), то есть на обкладках сосредоточен определенный заряд. Причем наибольший интерес представляет тот случай, когда заряды пластин конденсатора одинаковы по модулю и противоположны по знаку (как на рисунке).

А поскольку на обкладках сосредоточен заряд, между ними возникает электрическое поле. Поле плоского конденсатора, в основном, сосредоточено между пластинами, однако, в окружающем пространстве также возникает электрическое поле, которое называют полем рассеяния. Очень часто его влиянием в задачах пренебрегают, но забывать о нем не стоит.

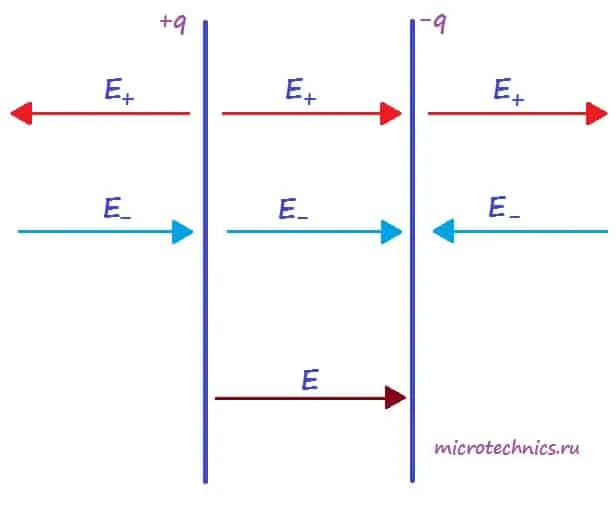
Для определения величины этого поля рассмотрим еще одно схематическое изображение плоского конденсатора:

Каждая из обкладок конденсатора в отдельности создает электрическое поле:

• положительно заряженная пластина (+q) создает поле, напряженность которого равна E_{+}
• отрицательно заряженная пластина (-q) создает поле, напряженность которого равна E_{-}

Выражение для напряженности поля равномерно заряженной пластины выглядит следующим образом:

E_{пл} = \frac{\sigma}{2\varepsilon_0\thinspace\varepsilon}

Здесь \sigma- это поверхностная плотность заряда: \sigma = \frac{q}{S}, а \varepsilon - диэлектрическая проницаемость диэлектрика, расположенного между обкладками конденсатора. Поскольку площадь пластин конденсатора у нас одинаковая, как и величина заряда, то и модули напряженности электрического поля, равны между собой:

E_+ = E_- = \frac{q}{2\varepsilon_0\thinspace\varepsilon S}

Но направления векторов разные - внутри конденсатора вектора направлены в одну сторону, а вне - в противоположные. Таким образом, внутри обкладок результирующее поле определяется следующим образом:

E = E_+ + E_- = \frac{q}{2\varepsilon_0\thinspace\varepsilon S} + \frac{q}{2\varepsilon_0\thinspace\varepsilon S} = \frac{q}{\varepsilon_0\thinspace\varepsilon S}

Соответственно, вне конденсатора (слева и справа от обкладок) поля пластин компенсируют друг друга и результирующая напряженность равна 0.

Процессы зарядки и разрядки конденсаторов.

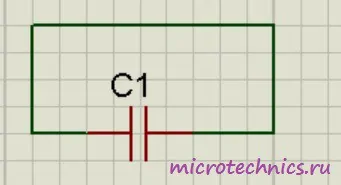
С устройством мы разобрались, теперь разберемся, что произойдет, если подключить к конденсатору источник постоянного тока. На принципиальных электрических схемах конденсатор обозначают следующим образом:

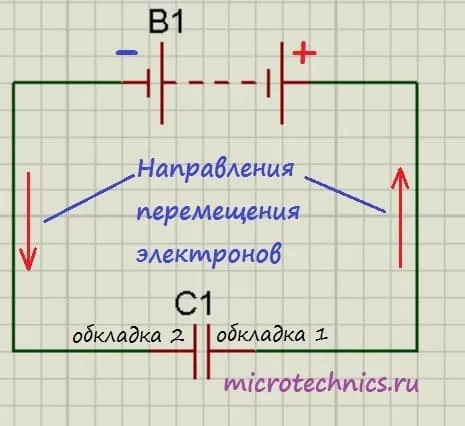
Итак, мы подключили обкладки конденсатора к полюсам источника постоянного тока. Что будет происходить?

Свободные электроны с первой обкладки конденсатора устремятся к положительному полюсу источника. Из-за этого на обкладке возникнет недостаток отрицательно заряженных частиц, и она станет положительно заряженной. В то же время электроны с отрицательного полюса источника тока переместятся ко второй обкладке конденсатора. В результате чего на ней возникнет избыток электронов, соответственно, обкладка станет отрицательно заряженной.

Таким образом, на обкладках конденсатора образуются заряды разного знака (как раз этот случай мы и рассматривали в первой части статьи), что приводит к появлению электрического поля, которое создаст между пластинами конденсатора определенную разность потенциалов. Процесс зарядки будет продолжаться до тех пор, пока эта разность потенциалов не станет равна напряжению источника тока. После этого процесс зарядки закончится, и перемещение электронов по цепи прекратится.

При отключении от источника конденсатор может на протяжении длительного времени сохранять накопленные заряды. Соответственно, заряженный конденсатор является источником электрической энергии, это означает, что он может отдавать энергию во внешнюю цепь. Давайте создадим простейшую цепь, просто соединив обкладки конденсатора друг с другом:

В данном случае по цепи начнет протекать ток разряда конденсатора, а электроны начнут перемещаться с отрицательно заряженной обкладки к положительной. В результате напряжение на конденсаторе (разность потенциалов между обкладками) начнет уменьшаться. Этот процесс завершится в тот момент, когда заряды пластин конденсаторов станут равны друг другу, соответственно электрическое поле между обкладками пропадет и по цепи перестанет протекать ток. Именно так происходит разряд конденсатора, в результате которого он отдает во внешнюю цепь всю накопленную энергию. Как видите, здесь нет ничего сложного.

Емкость и энергия конденсатора.

Важнейшей характеристикой является электрическая емкость конденсатора. Это физическая величина, которая определяется как отношение заряда q одного из проводников к разности потенциалов между проводниками:

C = \frac{q}{\Delta\varphi} = \frac{q}{U}

Емкость конденсатора изменяется в Фарадах, но величина 1 Ф является неимоверно большой, поэтому чаще всего используются микрофарады (мкФ), нанофарады (нФ) и пикофарады (пФ). А поскольку мы уже вывели формулу для расчета напряженности, то давайте выразим напряжение на конденсаторе следующим образом:

U = Ed = \frac{qd}{\varepsilon_0\thinspace\varepsilon S}

Здесь у нас d - это расстояние между пластинами конденсатора, а q - заряд конденсатора. Подставим эту формулу в выражение для емкости:

C = \frac{q\varepsilon_0\thinspace\varepsilon S}{qd} = \frac{\varepsilon_0\thinspace\varepsilon S}{d}

Если в качестве диэлектрика выступает воздух, то во всех формулах можно подставить \varepsilon = 1. Для запасенной же энергии конденсатора справедливы следующие выражения:

W = \frac{CU^2}{2} = \frac{qU}{2} = \frac{q^2}{2C}

Помимо емкости конденсаторы характеризуются еще одним параметром, а именно величиной напряжения, которое может выдержать его диэлектрик. При слишком больших значениях напряжения электроны диэлектрика отрываются от атомов, и диэлектрик начинает проводить ток. Это явление называется пробоем конденсатора, и в результате обкладки оказываются замкнутыми друг с другом. Собственно, характеристикой, которая часто используется при работе с конденсаторами является не напряжение пробоя, а рабочее напряжение. Это такая величина напряжения, при которой конденсатор может работать неограниченно долгое время, и пробоя не произойдет.

Итак, резюмируем - сегодня рассмотрели основные свойства конденсаторов, их устройство и характеристики, так что на этом заканчиваем статью, а в следующей мы будем обсуждать различные варианты соединений и маркировку.