Приветствую всех, сегодня в рамках курса "Основы электроники" мы рассмотрим основные способы измерения силы тока, напряжения и других параметров электрических цепей. Естественно, без внимания не останутся и основные измерительные приборы, такие как вольтметр и амперметр.
Измерение тока. Амперметр.
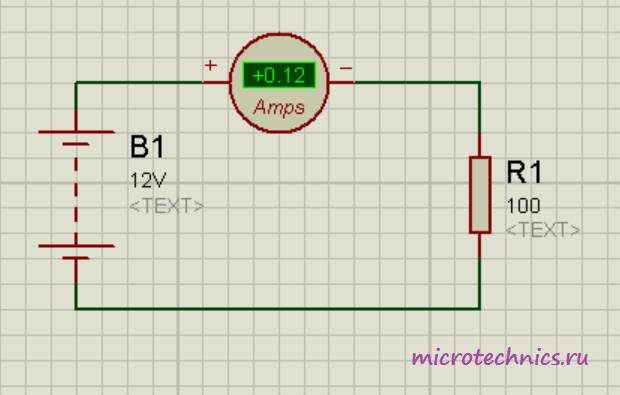
И начнем с измерения тока. Прибор, используемый для этих целей, называется амперметр, и в цепь он включается последовательно. Рассмотрим небольшой пример:
Как видите, здесь источник питания подключен напрямую к резистору, символизирующему полезную нагрузку. Кроме того, в цепи присутствует амперметр, включенный последовательно с резистором. По закону Ома сила тока в данной цепи:
I = \frac{U}{R} = \frac{12}{100} = 0.12Получили величину, равную 0.12 А, что в точности совпадает с практическим результатом, который демонстрирует амперметр в цепи 👍
Важным параметром этого прибора является его внутреннее сопротивление r_А. Почему это так важно? Смотрите сами - при отсутствии амперметра ток определяется по закону Ома, как мы и рассчитывали чуть выше. Но при наличии амперметра в цепи ток изменится, поскольку изменится общее сопротивление, и мы получим следующее значение:
I = \frac{U}{R_1+r_А}Если бы амперметр был абсолютно идеальным, и его сопротивление равнялось нулю, то он бы не оказал никакого влияния на работу электрической цепи, параметры которой необходимо измерить, но на практике все не совсем так, и сопротивление прибора не равно 0. Конечно, сопротивление амперметра достаточно мало (поскольку производители стремятся максимально его уменьшить), поэтому во многих примерах и задачах им пренебрегают, но не стоит забывать, что оно все-таки и есть и оно ненулевое.
При разговоре об измерении силы тока невозможно не упомянуть о способе, который позволяет расширить пределы, в которых может работать амперметр. Этот метод заключается в том, что параллельно амперметру включается шунт (резистор), имеющий определенное сопротивление:
R = \frac{r_А}{n\medspace-\medspace 1}В этой формуле n - это коэффициент шунтирования - число, которое показывает во сколько раз будут увеличены пределы, в рамках которых амперметр может производить свои измерения. Возможно это все может показаться не совсем понятным и логичным, поэтому сейчас мы рассмотрим практический пример, который позволит во всем разобраться.
Пусть максимальное значение, которое может измерить амперметр составляет 1 А. А схема, силу тока в которой нам нужно определить имеет следующий вид:
Отличие от предыдущей схемы заключается в том, что напряжение источника питания на этой схеме в 100 раз больше, соответственно, и ток в цепи станет больше и будет равен 12 А. Напряжение в 1200 В взято исключительно ради примера, сокровенного практического смысла в этом нет ) Итак, из-за ограничения на максимальное значение измеряемого тока напрямую использовать наш амперметр мы не сможем. Так вот для таких задач и нужно использовать дополнительный шунт:
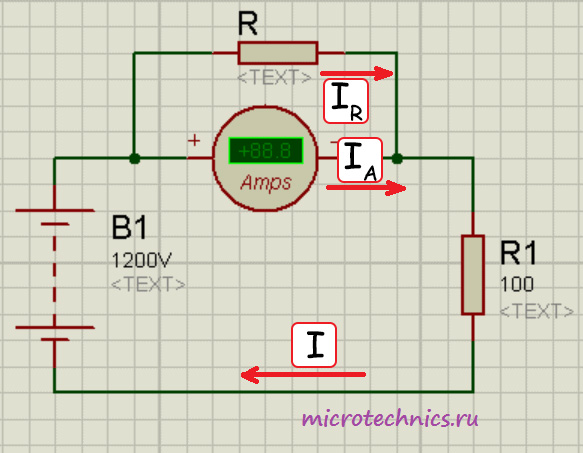
В данной задаче нам необходимо измерить ток I. Мы предполагаем, что его значение превысит максимально допустимую величину для используемого амперметра, поэтому добавляем в схему еще один элемент, который будет выполнять роль шунта. Пусть мы хотим увеличить пределы измерения амперметра в 25 раз, это значит, что прибор будет показывать значение, которое в 25 раз меньше, чем величина измеряемого тока. Нам останется только умножить показания прибора на известное нам число и получим нужное значение. Для реализации задумки мы должны поставить шунт параллельно амперметру, причем сопротивление его должно быть равно значению, которое мы определяем по формуле:
R = \frac{r_А}{n\medspace-\medspace 1}В данном случае n = 25, но мы проведем все расчеты в общем виде, чтобы показать, что величины могут быть абсолютно любыми, принцип шунтирования будет работать одинаково.
Итак, поскольку напряжения на шунте и на амперметре равны, мы можем записать первое уравнение:
I_А\medspace r_А = I_R\medspace R
Выразим ток шунта через ток амперметра:
I_R = I_А\medspace \frac{r_А}{R}Измеряемый ток равен:
I = I_R + I_А
Подставим в это уравнение предыдущее выражение для тока шунта:
I = I_А + I_А\medspace \frac{r_А}{R}Но сопротивление шунта нам также известно (R = \frac{r_А}{n\medspace-\medspace 1}). В итоге мы получаем:
I = I_А\medspace (1 + \frac{r_А\medspace (n\medspace-\medspace 1)}{r_А}\enspace) = I_А\medspace nВот мы и получили то, что и хотели. Значение, которое покажет амперметр в данной цепи будет в n раз меньше, чем сила тока, величину которой нужно измерить.
С измерениями тока в цепи все понятно, давайте перейдем к следующему вопросу, а именно определению напряжения.
Измерение напряжения. Вольтметр.
Прибор, предназначенный для измерения напряжения, называется вольтметр. И, в отличие от амперметра, в цепь он включается параллельно участку цепи, напряжение на котором необходимо определить. И, опять же, в противоположность идеальному амперметру, имеющему нулевое сопротивление, сопротивление идеального вольтметра должно быть равно бесконечности. Давай разберемся, с чем это связано:
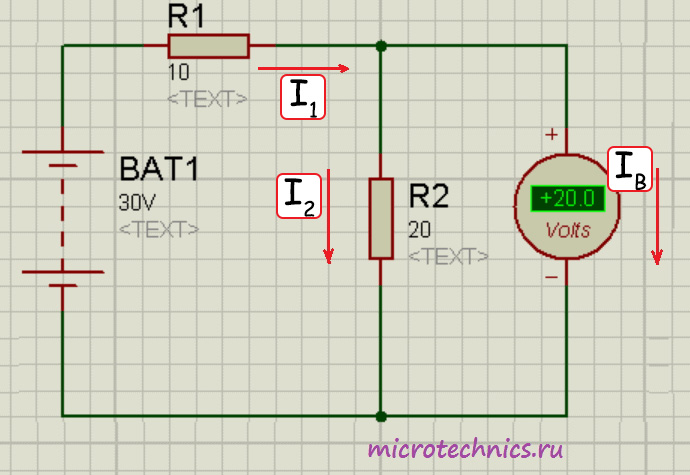
Если бы в цепи не было вольтметра, ток через резисторы был бы один и тот же и определялся по Закону Ома следующим образом:
I_1 = I_2 = \frac{U}{R_1 + R_2} = \frac{30}{10 + 20} = 1Итак, величина тока составила бы 1 А, а соответственно напряжение на резисторе 2 было бы равно 20 В. С этим все понятно, а теперь мы хотим измерить это напряжение вольтметром и включаем его параллельно с R_2. Если бы сопротивление вольтметра было бы бесконечно большим, то через него просто не потек бы ток (I_B = 0), и прибор не оказал бы никакого воздействия на исходную цепь. Но поскольку r_В имеет конечную величину и не равно бесконечности, то через вольтметр потечет ток. В связи с этим напряжение на резисторе R_2 уже не будет таким, каким бы оно было при отсутствии измерительного прибора. Вот поэтому идеальным был бы такой вольтметр, через который не проходил бы ток.
Как и в случае с амперметром, есть специальный метод, который позволяет увеличить пределы измерения напряжения для вольтметра. Для осуществления этого необходимо включить последовательно с прибором добавочное сопротивление, величина которого определяется по формуле:
R_Д = r_В\medspace (n\medspace-\medspace 1)
Это приведет к тому, что показания вольтметра будут в n раз меньше, чем значение измеряемого напряжения. По традиции давайте рассмотрим небольшой практический пример:
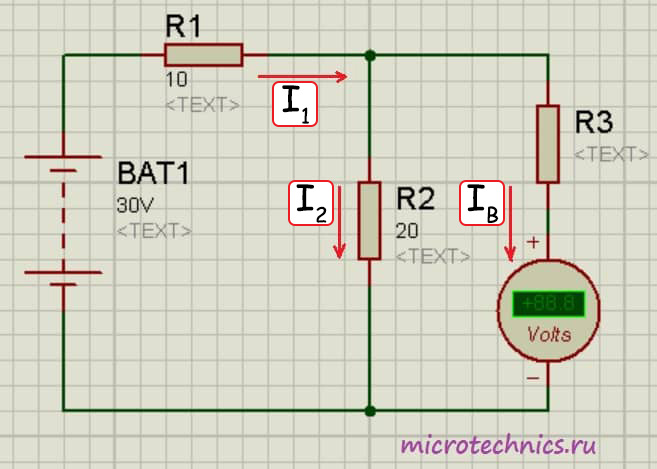
Здесь мы добавили в цепь добавочное сопротивление R_3. Перед нами стоит задача измерить напряжение на резисторе R_2:\medspace U_2 = R_2\medspace I_2. Давайте определим, какой результат при таком включении выдаст нам вольтметр:
U_2 = I_2\medspace R_2 = U_В + I_В\medspace R_3
Подставим в эту формулу выражение для расчета сопротивления добавочного резистора:
U_2 = U_В + I_В\medspace (r_В\medspace (n\medspace-\medspace 1)) = U_В + I_В\medspace r_В\medspace n\medspace-\medspace I_В\medspace r_В = U_В + U_В\medspace n\medspace-\medspace U_В = U_В\medspace n
Таким образом: U_В = \frac{U_2}{n}. То есть показания вольтметра будут в n раз меньше, чем величина напряжения, которое мы измеряли. Так что, используя данный метод, возможно значительно увеличить пределы измерения вольтметра.
В завершении статьи пару слов об измерении сопротивления и мощности.
Для решения обеих задач возможно совместное использование амперметра и вольтметра. В предыдущих статьях (про мощность и сопротивление) мы подробно останавливались на понятиях сопротивления и мощности и их связи с напряжением и сопротивлением, таким образом, зная ток и напряжение электрической цепи можно произвести расчет нужного нам параметра. Ну а кроме того есть специальные приборы, которые позволяют произвести измерения сопротивления участка цепи (омметр) и мощности (ваттметр).
В общем-то, на этом, пожалуй, на сегодня закончим, следите за обновлениями!