При обсуждении переменного тока в одной из предыдущих статей (ссылка) мы познакомились с понятием гармонической (синусоидальной) функции. А бывают ли негармонические функции и сигналы, и как с ними работать? В этом нам и предстоит сегодня разобраться. Кроме того, мы рассмотрим важнейшее понятие - амплитудно-частотную характеристику (АЧХ) сигналов.
Гармонические и негармонические сигналы.
И для начала чуть подробнее разберемся, как классифицируются сигналы. В первую очередь, нас интересуют периодические сигналы. Их форма повторяется через определенный интервал времени T, называемый периодом. Периодические сигналы в свою очередь делятся на два больших класса - гармонические и негармонические. Гармонический сигнал - это сигнал, который можно описать следующей функцией:
y = A cos(wt + \phi)
Здесь A - амплитуда сигнала, w - циклическая частота, а \phi - начальная фаза. Может возникнуть логичный вопрос - разве синусоидальный сигнал не является гармоническим? Конечно, является, дело в том, что sin\alpha = cos(\frac{\pi}{2}\medspace-\medspace \alpha) - то есть сигналы отличаются начальной фазой, соответственно, синусоидальный сигнал не противоречит определению, которое мы дали для гармонических колебаний.
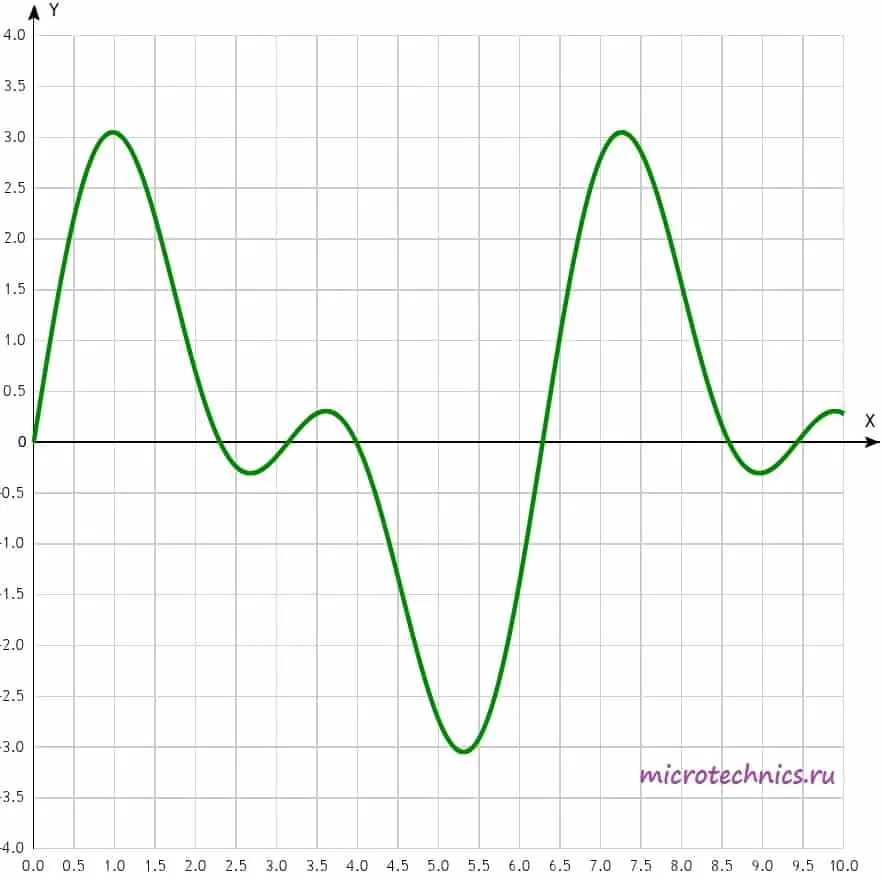
Вторым подклассом периодических сигналов являются негармонические колебания. Вот пример негармонического сигнала:
Как видите, несмотря на свой вид, сигнал остается периодическим, то есть его форма повторяется через интервал времени, равный периоду.
Для работы с такими сигналами и их исследования существует определенная методика, которая заключается в разложении сигнала в ряд Фурье. Суть состоит в том, что негармонический периодический сигнал (при выполнении определенных условий) можно представить в виде суммы гармонических колебаний с определенными амплитудами, частотами и начальными фазами. Важным нюансом является то, что все гармонические колебания, которые участвуют в суммировании, должны иметь частоты, кратные частоте исходного негармонического сигнала. Возможно это пока не совсем понятно, так что рассмотрим практический пример и разберемся подробнее. И для примера используем сигнал, который изображен на рисунке чуть выше. Его можно представить следующим образом:
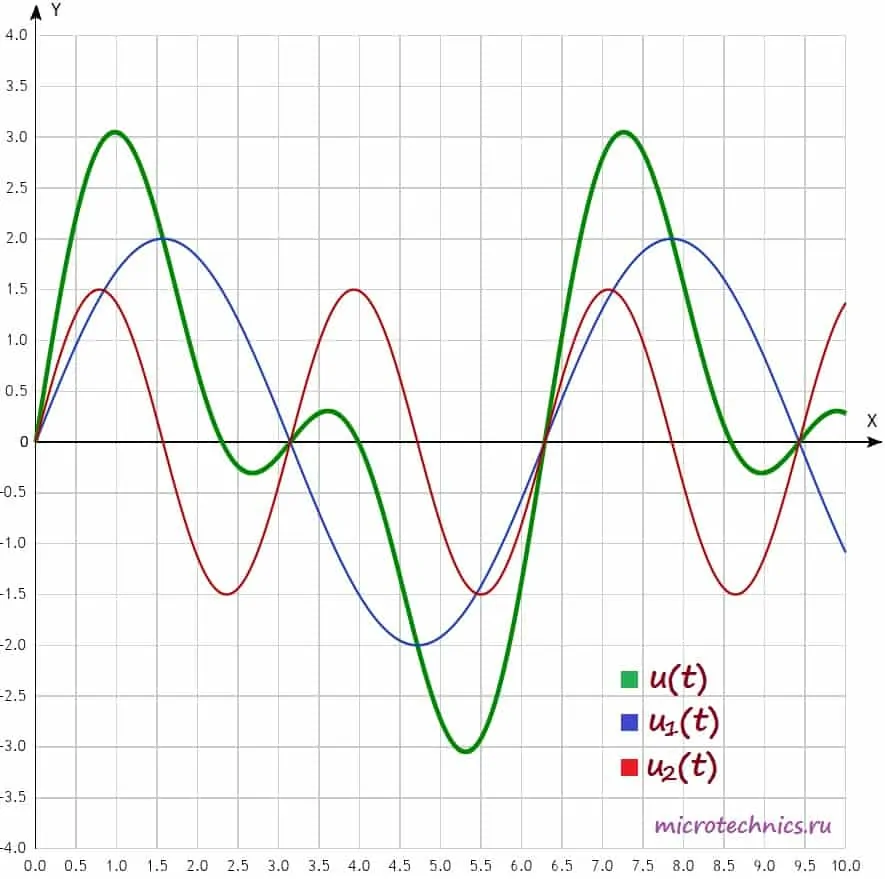
u(t) = u_1(t) + u_2(t) = 2 sin(t) + 1.5 sin(2t)
Давайте изобразим все эти сигналы на одном графике:
Функции u_1(t), u_2(t) называют гармониками сигнала, а ту из них, период которой равен периоду негармонического сигнала, называют первой или основной гармоникой. В данном случае первой гармоникой является функция u_1(t) (ее частота равна частоте исследуемого негармонического сигнала, соответственно, равны и их периоды). А функция u_2(t) = 1.5 sin(2t) представляет из себя ни что иное как вторую гармонику сигнала (ее частота в два раза больше). В общем случае, негармонический сигнал раскладывается на бесконечное число гармоник:
u(t) = U_0 + \sum_{i=0}^{\infty}{U_{k}\thinspace sin(\thinspace kwt + \phi_k\thinspace )}Здесь U_k - амплитуда, а \phi_k - начальная фаза k-ой гармоники. Как мы уже упомянули чуть ранее, частоты всех гармоник кратны частоте первой гармоники, собственно, это мы и наблюдаем в данной формуле. U_0 - это нулевая гармоника, ее частота равна 0, она равна среднему значению функции за период. Почему среднему? Смотрите - среднее значения функции синуса за период равно 0, а значит при усреднении в этой формуле все слагаемые, кроме U_0 будут равны 0 👍
Амплитудный спектр сигнала.
Совокупность всех гармонических составляющих негармонического сигнала называют спектром этого сигнала. Различают фазовый и амплитудный спектр сигнала:
- фазовый спектр сигнала - совокупность начальных фаз всех гармоник
- амплитудный спектр сигнала - амплитуды всех гармоник, из которых складывается негармонический сигнал
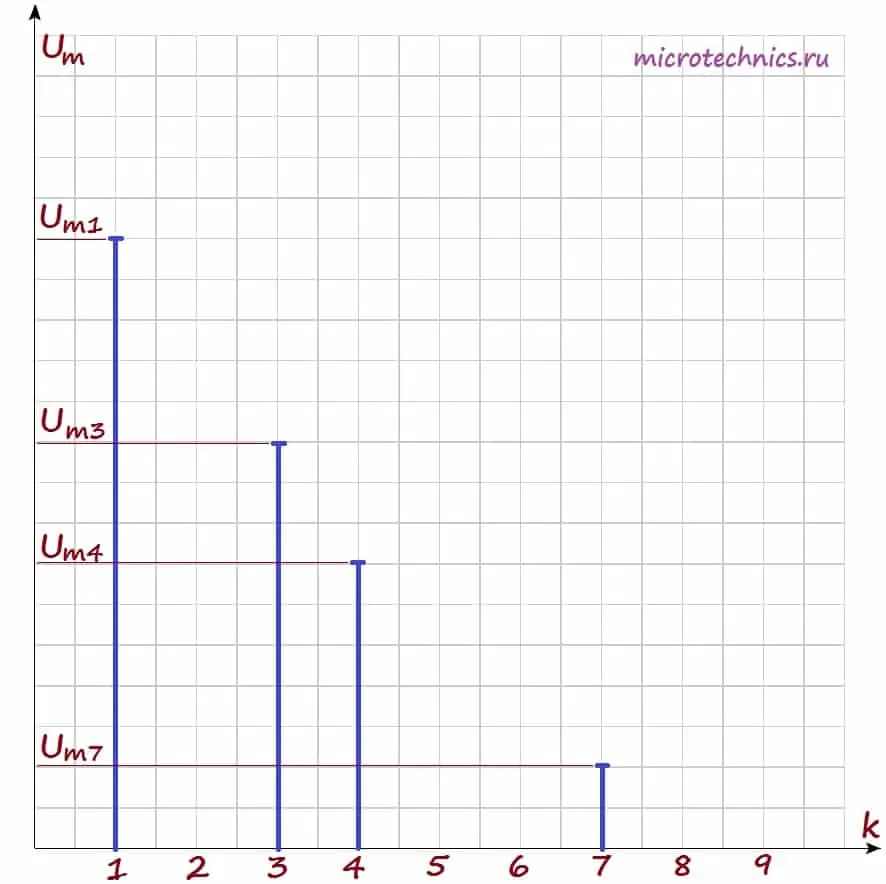
Давайте рассмотрим амплитудный спектр подробнее. Для визуального изображения спектра используют диаграммы, представляющие из себя набор вертикальных линий определенной длины (длина зависит от амплитуды сигналов). На горизонтальной оси диаграммы откладываются частоты гармоник:
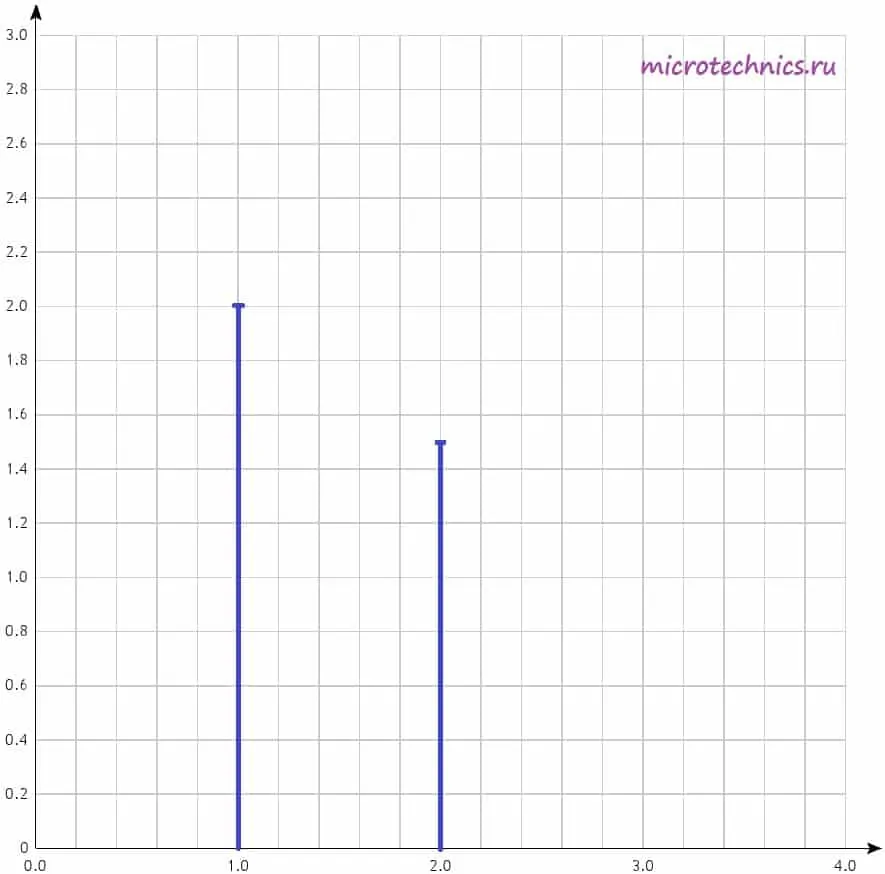
При этом на горизонтальной оси могут откладываться как частоты в Гц, так и просто номера гармоник, как в данном случае. А по вертикальной оси - амплитуды гармоник, тут все понятно. Давайте построим амплитудный спектр сигнала для негармонического колебания, которое мы рассматривали в качестве примера в самом начале статьи. Напоминаю, что его разложение в ряд Фурье выглядит следующим образом:
u(t) = u_1(t) + u_2(t) = 2 sin(t) + 1.5 sin(2t)
У нас есть две гармоники, амплитуды которых равны, соответственно, 2 и 1.5. Поэтому на диаграмме две линии, длины которых соответствуют амплитудам гармонических колебаний. Фазовый спектр сигнала строится аналогично, за той лишь разницей, что используются начальные фазы гармоник, а не амплитуды.
Итак, с построением и анализом амплитудного спектра сигнала мы разобрались. Давайте перейдем к следующей теме сегодняшней статьи - к понятию амплитудно-частотной характеристики.
Амплитудно-частотная характеристика (АЧХ).
АЧХ является важнейшей характеристикой многих цепей и устройств - фильтров, усилителей звука и т. д. Даже простые наушники имеют свою собственную амплитудно-частотную характеристику. Проанализируем, какой смысл она в себе несет...
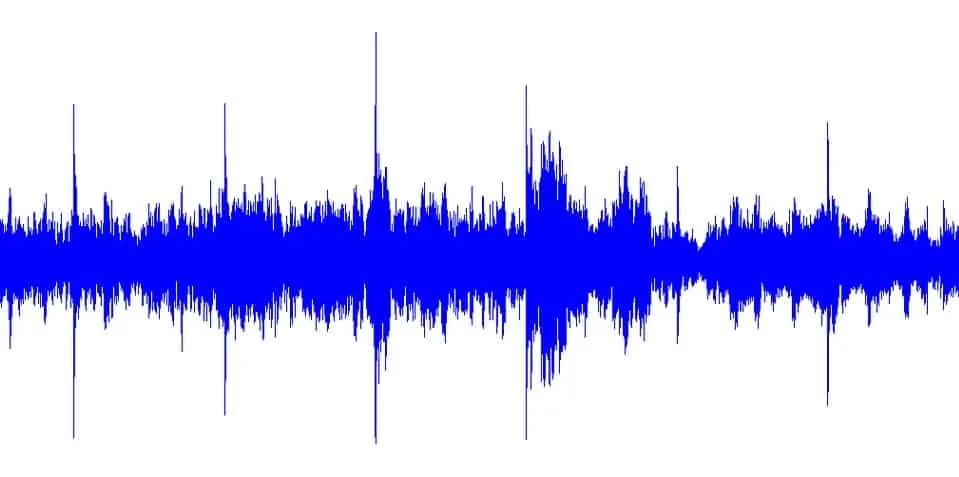
АЧХ - это зависимость амплитуды выходного сигнала от частоты входного сигнала. Как мы выяснили в первой части статьи, негармонический периодический сигнал можно разложить в ряд Фурье. Но мы сейчас рассмотрим, в первую очередь, аудио-сигнал, и выглядит он следующим образом:
Как видите, ни о какой периодичности здесь не идет и речи. Но, к счастью, существуют специальные алгоритмы, которые позволяют представить звуковой сигнал в виде спектра входящих в него частот. Мы сейчас не будем подробно разбирать эти алгоритмы, это тема для отдельной статьи. Просто примем тот факт, что они позволяют нам осуществить такое преобразование.
Соответственно, мы можем построить диаграмму амплитудного спектра такого сигнала. А пройдя через какую-либо цепь (к примеру, через наушники при воспроизведении звука) сигнал будет изменен. Так вот амплитудно-частотная характеристика как раз и показывает, какие изменения будет претерпевать входной сигнал при прохождении через ту или иную цепь. Давайте детально обсудим этот момент.
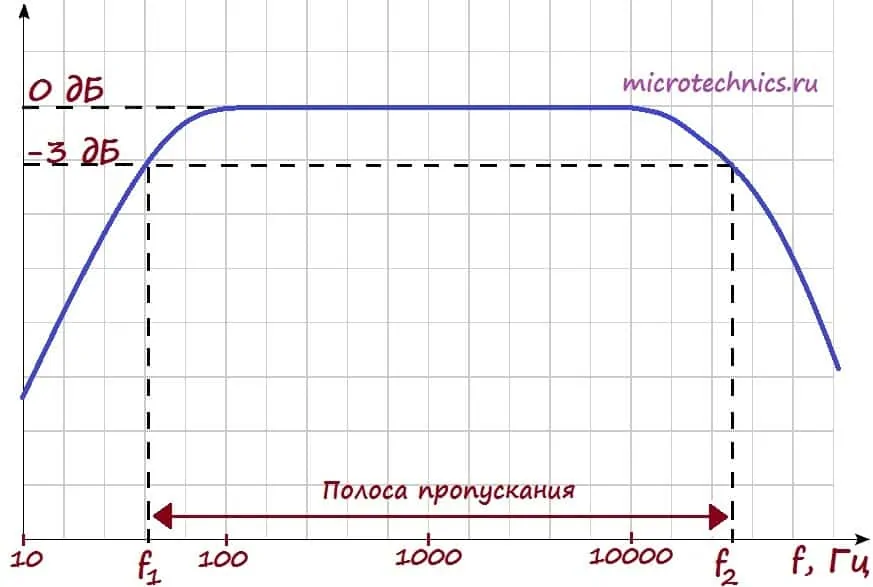
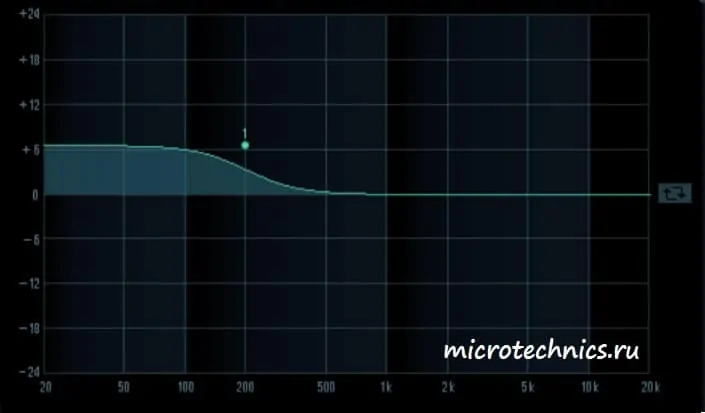
Итак, на входе мы имеем ряд гармоник. Амплитудная-частотная характеристика показывает, как изменится амплитуда той или иной гармоники при прохождении через цепь. Рассмотрим пример АЧХ:
Разбираем поэтапно, что тут изображено. Начнем с осей графика АЧХ. По оси y мы откладываем величину выходного напряжения (или коэффициента усиления, как на данном рисунке). Коэффициент усиления мы считаем в дБ, соответственно величина, равная 0 дБ, соответствует усилению в 1 раз, то есть амплитуда сигнала остается неизменной.
По оси x откладываются частоты входного сигнала. Таким образом, в рассматриваемом случае для всех гармоник, частоты которых лежат в интервале от 100 до 10000 Гц, амплитуда не изменится. А сигналы всех остальных гармоник будут ослаблены.
На графике отдельно отмечены частоты f_1 и f_2. Их отличительной особенностью является то, что сигнал гармоник данных частот будет ослаблен в 1.41 раза (3 дБ) по напряжению. Это соответствует уменьшению по мощности в 2 раза . Полосу частот между f_1 и f_2 называют полосой пропускания. Получается следующая ситуация - сигналы всех гармоник, частоты которых лежат в пределах полосы пропускания устройства/цепи будут ослаблены менее, чем в 2 раза по мощности.
Практические примеры АЧХ аудио-устройств.
Частотный диапазон аудио-устройств обычно разбивают на низкие, средние и высокие частоты. Приблизительно это выглядит так:
- 20 Гц - 160 Гц - область низких частот
- 160 Гц - 1.28 КГц - область средних частот
- 1.28 КГц - 20.5 КГц - область высоких частот
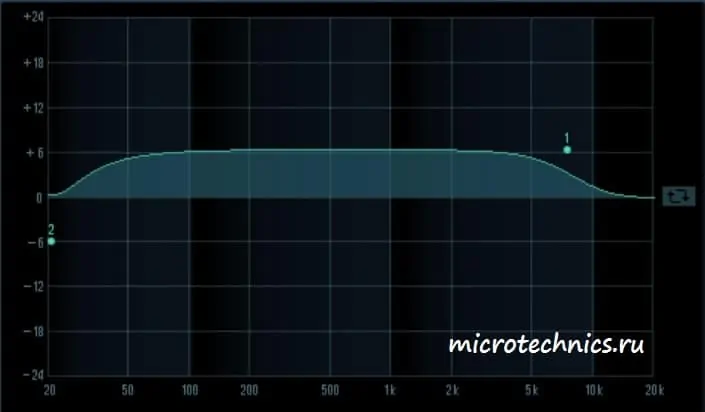
Именно такую терминологию обычно можно встретить в разных программах-эквалайзерах, используемых для настройки звука. Теперь вы знаете, что красивые графики из таких программ являются именно амплитудно-частотными характеристиками, с которыми мы познакомились в сегодняшней статье. И в завершение статьи посмотрим на пару примеров АЧХ:
Здесь мы можем видеть амплитудно-частотную характеристику усилителя. Причем усилены будут преимущественно средние частоты диапазона.
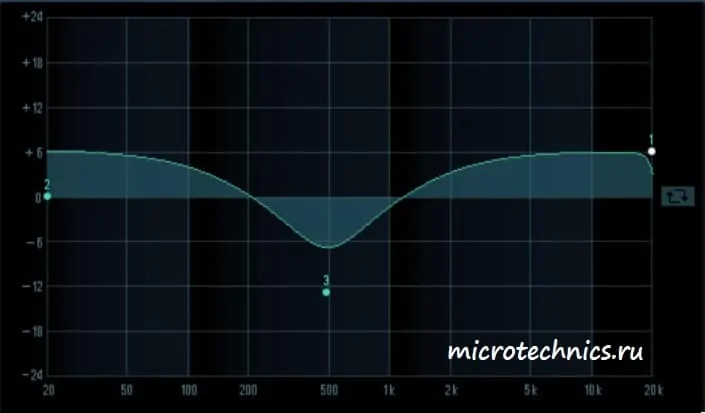
Во втором случае ситуация совсем другая - низкие и верхние частоты усиливаются, а в области средних частот для гармоник с частотой 500 Гц мы наблюдаем значительное ослабление.
А теперь усиливаются только низкие частоты. Аудио-аппаратура с такой АЧХ будет обладать высоким уровнем басов.
На этом мы и заканчиваем нашу сегодняшнюю статью. Спасибо за внимание и ждем вас на нашем сайте снова 🤝











Как всегда, все просто и понятно)) Большое спасибо за Ваши статьи!!!
Теперь ждем статью по этой теме: "Мы сейчас не будем подробно разбирать эти алгоритмы, это тема для отдельной статьи" 🙂
Спасибо за хороший отзыв!!! =)
Периодически захожу на ваш сайт в ожидании новый статей про stm32. Планируются?
Да, конечно. Планировалось осенью, но отложилось, теперь зимой должны выйти статьи.
Супер, в запой читал, доступно и подробно, 10 из 10
Спасибо за отличный отзыв!
АЧХ - это модуль передаточной характеристики.
Ай-яй-яй, вот уже прошёл 1 год, как нет новых статей!!! Пора исправляться!!!
Что тут сказать.... Согласен )
Большое спасибо! Сатья очень помогла собрать имещиеся занания в стройную модель).
Рад, что статья оказалась полезной! =)
Спасибо большое за простоту и наглядность!
Благодарю за отличный отзыв!
Хорошая статья! Спасибо! Надеюсь на ваше дальнейшее развитие, чтоб читать и другие статьи)
Большое спасибо!
Браво!
Круто, в институтах бы так объясняли.
Спасибо!
Добрый день, а новые статьи планируются?
Добрый день!
Да, скоро сайт возобновит полноценную работу, будет много новых статей, и больше длительных пауз в статьях не предвидится =)
Хотелось бы уже новых статей. Автор пропал на 4 года
Будут... =)
Можно ли расписать алгоритм построения ачх через бпф? Где какие размерности, в какой момент логарифмируется, где отсчеты переходят в герцы и тд.
Где тут лайки можно поставить??? Наконец - то я понял, хотя уже не одну статью и книгу прочитал. Буквально с первых двух предложений.
Благодарю за отзыв)
у вас есть спектры. Смотрите на них. чему соответствуют вертикальные линии на спектрах?
Вы чо дураки??? НАс это на уроке заставляют учить, удаляйте быстро!!!