Трехфазные электрические цепи.

Сегодня мы вернемся к обсуждению основ электроники (ссылка) и обсудим наиболее распространенные в современной энергетике цепи, а именно трехфазные. По сути, приходящее к каждому из нас в квартиру однофазное напряжение (те самые 220 В) есть ни что иное, как одна из фаз от генерируемого на электростанции трехфазного напряжения ) Собственно, в этой статье мы рассмотрим некоторые математические аспекты данного вопроса, а также рассмотрим, какой же смысл кроется в использовании именно таких сигналов.

Начнем сразу с преимуществ использования трехфазных цепей. А это, в первую очередь, простота и экономичность генерации. А как, собственно, генерировать переменный трехфазный ток?

Для создания цепи необходимы три источника напряжения с одинаковыми частотами и амплитудами, но смещенные друг относительно друга по фазе на 120 градусов. С поставленной задачей отлично справляется синхронный генератор, выполненный по следующей схеме:

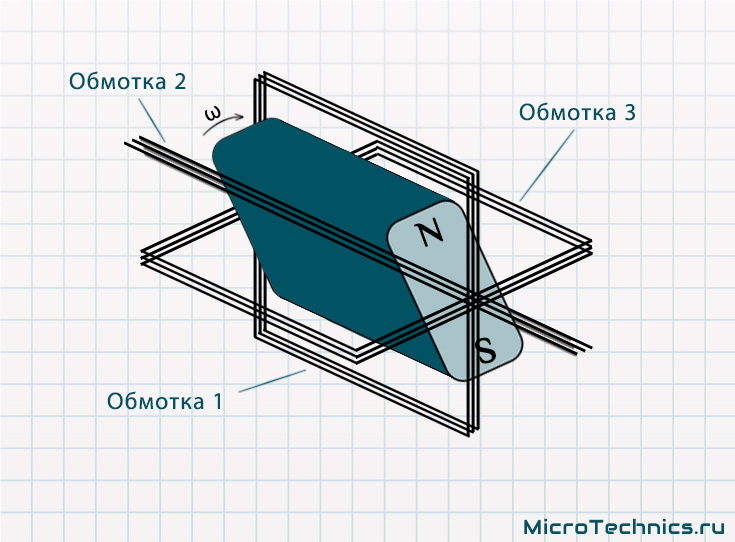
Генератор состоит из двух частей – ротора и статора – подвижной и неподвижной частей. На статоре расположены три абсолютно одинаковые обмотки, смещенные друг относительно друга на 120 градусов (360 / 3). Ротор же представляет из себя электромагнит, создающий вокруг себя магнитное поле. Суть заключается в том, что при вращении ротора положение магнитного поля и обмоток друг относительно друга меняется, в результате чего в обмотках наводятся синусоидальные сигналы. Для трехфазного напряжения нам нужны синусоидальные напряжения с одинаковой частотой и амплитудой, но отличающиеся по фазе. В данном случае у нас равенство амплитуд гарантируется абсолютной идентичностью конструкции обмоток генератора. Частота сигналов зависит от частоты вращения ротора, а смещение сигналов по фазе обеспечивается тем, что обмотки смещены друг относительно друга в пространстве. Собственно, вот так, в общих чертах, работают генераторы трехфазного напряжения 😉

В итоге мы получаем на обмотках:

$e_1 = E_msin(wt)$

$e_2 = E_msin(wt - 2\pi / 3)$

$e_3 = E_msin(wt - 4\pi / 3) = E_msin(wt + 2\pi / 3)$

Если записать действующие значения ЭДС в комплексном виде, то получим следующее:

$E_1 = E_me^{j*0}$

$E_2 = E_me^{j*(-120)}$

$E_3 = E_me^{j*120}$

В конце статьи мы обязательно построим векторную диаграмму для этих величин.

Чаще всего, кстати, обозначают $E_1$ , $E_2$ и $E_3$ как $E_A$ , $E_B$ и $E_C$ . Пожалуй и мы тоже будем придерживаться такой системы обозначений )

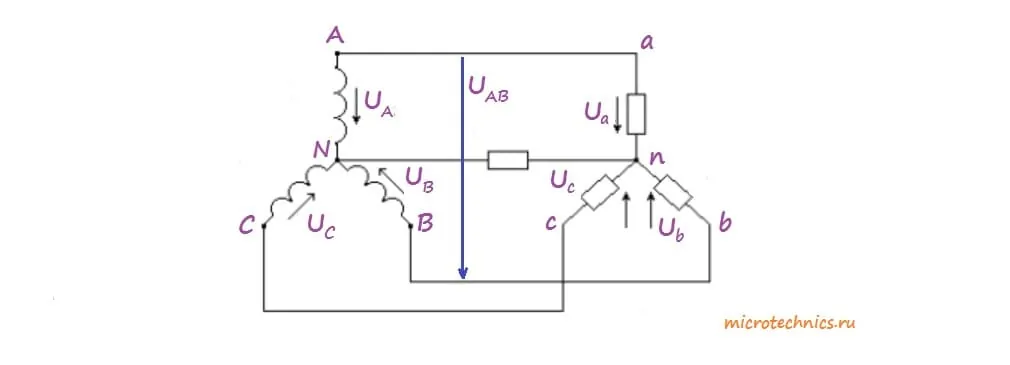
Давайте перейдем к рассмотрению практического примера подключения потребителя к трехфазной цепи. И тут наиболее “популярным” способом является соединение звездой:

Точки A, B и С (начала фаз) соединены с точками a, b и c потребителя. А концы фаз в свою очередь соединены все вместе (точка N) и подключены к точке n приемника. Таким образом, требуется всего 4 провода, которые называются соответственно линейными (A-a, B-b, C-c) и нейтральным (N-n).

На заре развития трехфазных цепей концы фаз не соединялись вместе, а просто подключались к концам фаз приемника. В итоге по сути получались три однофазные цепи и для подключения требовалось 6 проводов, а не 4. В связи с экономической невыгодностью такое подключение практически не используется.

Давайте теперь на примере соединения звездой рассмотрим некоторые основные термины, использующиеся при работе с такими цепями. В трехфазной цепи различают понятия линейных и фазных напряжений и токов. Фазное напряжение – это напряжение между линейным проводом и нейтральным ( $U_A$ , $U_B$ , $U_C$ , $U_a$ , $U_b$ , $U_c$ ). Если пренебрегать собственным сопротивлением соединительных проводов, то фазные напряжения приемника равны соответствующим фазным напряжениям источника ( $U_a = U_A$ , $U_b = U_B$ , $U_c = U_C$ ).

Линейным же напряжением называют напряжение между линейными проводами разных фаз, например $U_{AB}$ , как на нашей схеме. Аналогично можно определить $U_{CA}$ и $U_{BC}$ ).

И вот как раз-таки еще одним важным преимуществом трехфазных цепей является возможность получения двух величин напряжения в одном генераторе. Давайте определим, собственно, значения этих напряжений.

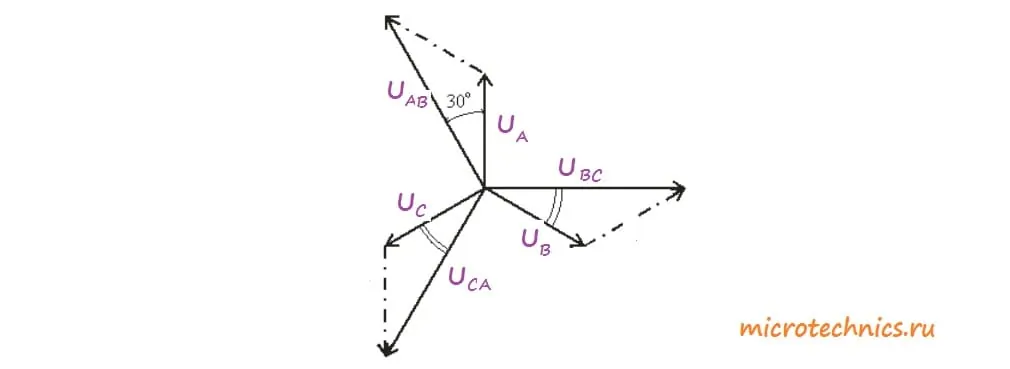
Зная, что сигналы $U_A$ , $U_B$ и $U_C$ смещены друг относительно друга на 120 градусов, а также учитывая условно выбранные направления напряжений получим следующие уравнения для векторов напряжений (мы рассматриваем именно вектора, а не действующие значения, нельзя путать эти понятия (!)):

$U_{AB} = U_A - U_B$

$U_{BC} = U_B - U_C$

$U_{CA} = U_C - U_A$

Построим векторную диаграмму:

Отсюда геометрически очень просто получить следующее уравнение связи линейных и фазных напряжений:

$U_{AB} = 2U_Acos(30)$

Немного упростим и получим:

$U_{AB} = \sqrt3U_A$

Поскольку фазные напряжения у нас являются переменными и изменяющимися по синусоидальному закону, то и линейное напряжение будет синусоидальным. Причем связаны фазное и линейное напряжения будут полученным выше соотношением.

Рассмотрим “бытовую” трехфазную цепь. К нам в квартиру приходит одна из трех фаз, которая представляет из себя переменное напряжение с действующим значением равным 220В. Каким бы в данном случае было действующее значение линейного напряжения, если бы к нам в квартиру приходили все три фазы? А все просто: 220В * $\sqrt3$ = 380В 😉

На этом мы на сегодня заканчиваем, надеюсь статья окажется понятной и полезной. До скорых встреч!

Трехфазные электрические цепи.: 4 комментария

Дмитрий говорит 13.03.2015 в 06:46:

Всё просто и понятно. Вроде даже понятнее, чем из школьного учебника физики) Единственное замечание: ротором всё же на электростанциях является не магнит, а электромагнит – обмотка возбуждения, на которую подаётся ток.

Ответить ↓
Nemo говорит 13.03.2015 в 19:46:

А о соединении треугольником будете писать?

Ответить ↓
- Aveal говорит 13.03.2015 в 19:56:
  
  Вообще, честно говоря, не собирался )
  
  Ответить ↓
Вячеслав говорит 20.04.2015 в 08:56:

Хорошая статья. Читал с удовольствием. Я сам не электрик, хотя в дипломе значится “Инженер электрик”. Но когда я знакомлюсь с каким-нибудь электриком, у меня к нему есть 2 вопроса. Первый – почему в трехфазной цепи между фазой и нулем 220в, а между двумя любыми фазами 380в, а не 440в. 90% электриков не могут ответить на вопрос. И второй вопрос-просьба – нарисовать проходной выключатель. Я такой выключатель придумал и реализовал дома классе в 7. Увидел у друга. Долго ломал голову, пока друг мне не сказал, что отец что-то там в выключателях переделал. Процентов 50 электриков не могут нарисовать такую схему. Это когда длинный коридор и два выключателя – в начале и в конце. Работают независимо друг от друга.

Ответить ↓