Рад снова всех приветствовать, и сегодня продолжим планомерно двигаться в выбранном направлении. Речь, конечно, о масштабном разборе искусственных нейронных сетей для решения широкого спектра задач. Продолжим ровно с того момента, на котором остановились в предыдущей части, и это означает, что героем данного поста будет ключевой процесс - обучение нейронных сетей.
Тема эта крайне важна, поскольку именно процесс обучения позволяет сети начать выполнять задачу, для которой она, собственно, и предназначена. То есть нейронная сеть функционирует не по какому-либо жестко заданному на этапе проектирования алгоритму, она совершенствуется в процессе анализа имеющихся данных. Этот процесс и называется обучением нейронной сети. Математически суть процесса обучения заключается в корректировке значений весов синапсов (связей между имеющимися нейронами). Изначально значения весов задаются случайно, затем производится обучение, результатом которого будут новые значения синаптических весов. Это все мы максимально подробно разберем как раз в этой статье.
На своем сайте я всегда придерживаюсь концепции, при которой теоретические выкладки по максимуму сопровождаются практическими примерами для максимальной наглядности. Так мы поступим и сейчас 👍
Итак, суть заключается в следующем. Пусть у нас есть простейшая нейронная сеть, которую мы хотим обучить (продолжаем рассматривать сети прямого распространения):

То есть на входы нейронов I1 и I2 мы подаем какие-либо числа, а на выходе сети получаем соответственно новое значение. При этом нам необходима некая выборка данных, включающая в себя значения входов и соответствующее им, правильное, значение на выходе:
| \bold{I_1} | \bold{I_2} | \bold{O_{net}} |
|---|---|---|
| x_{11} | x_{12} | y_{1} |
| x_{21} | x_{22} | y_{2} |
| x_{31} | x_{32} | y_{3} |
| ... | ... | ... |
| x_{N1} | x_{N2} | y_{N} |
Допустим, сеть выполняет суммирование значений на входе, тогда данный набор данных может быть таким:
| \bold{I_1} | \bold{I_2} | \bold{O_{net}} |
|---|---|---|
| 1 | 4 | 5 |
| 2 | 7 | 9 |
| 3 | 5 | 8 |
| ... | ... | ... |
| 1000 | 1500 | 2500 |
Эти значения и используются для обучения сети. Как именно - рассмотрим чуть ниже, пока сконцентрируемся на идее процесса в целом. Для того, чтобы иметь возможность тестировать работу сети в процессе обучения, исходную выборку данных делят на две части - обучающую и тестовую. Пусть имеется 1000 образцов, тогда можно 900 использовать для обучения, а оставшиеся 100 - для тестирования. Эти величины взяты исключительно ради наглядности и демонстрации логики выполнения операций, на практике все зависит от задачи, размер обучающей выборки может спокойно достигать и сотен тысяч образцов.
Итак, итог имеем следующий - обучающая выборка прогоняется через сеть, в результате чего происходит настройка значений синаптических весов. Один полный проход по всей выборке называется эпохой. И опять же, обучение нейронной сети - это процесс, требующий многократных экспериментов, анализа результатов и творческого подхода. Все перечисленные параметры (размер выборки, количество эпох обучения) могут иметь абсолютно разные значения для разных задач и сетей. Четкого правила тут просто нет, в этом и кроется дополнительный шарм и изящность )
Возвращаемся к разбору, и в результате прохода обучающей выборки через сеть мы получаем сеть с новыми значениями весов синапсов.
Далее мы через эту, уже обученную в той или иной степени, сеть прогоняем тестовую выборку, которая не участвовала в обучении. При этом сеть выдает нам выходные значения для каждого образца, которые мы сравниваем с теми верными значениями, которые имеем.
Анализируем нашу гипотетическую выборку:

Таким образом, для тестирования подаем на вход сети значения x_{(M+1)1}, x_{(M+1)2} и проверяем, чему равен выход, ожидаем очевидно значение y_{(M+1)}. Аналогично поступаем и для оставшихся тестовых образцов. После чего мы можем сделать вывод, успешно или нет работает сеть. Например, сеть дает правильный ответ для 90% тестовых данных, дальше уже встает вопрос - устраивает ли нас данная точность или процесс обучения необходимо повторить, либо провести заново, изменив какие-либо параметры сети.
В этом и заключается суть обучения нейронных сетей, теперь перейдем к деталям и конкретным действиям, которые необходимо осуществить для выполнения данного процесса. Двигаться снова будем поэтапно, чтобы сформировать максимально четкую и полную картину. Поэтому начнем с понятия градиентного спуска, который используется при обучении по методу обратного распространения ошибки. Обо всем этом далее…
Обучение нейронных сетей. Градиентный спуск.
Рассмотрев идею процесса обучения в целом, на данном этапе мы можем однозначно сформулировать текущую цель - необходимо определить математический алгоритм, который позволит рассчитать значения весовых коэффициентов таким образом, чтобы ошибка сети была минимальна. То есть грубо говоря нам необходима конкретная формула для вычисления:
\Delta w_{ij} = f(...)Здесь \Delta w_{ij} - величина, на которую необходимо изменить вес синапса, связывающего нейроны i и j нашей сети. Соответственно, зная это, необходимо на каждом этапе обучения производить корректировку весов связей между всеми элементами нейронной сети. Задача ясна, переходим к делу.
Пусть функция ошибки от веса имеет следующий вид:
E = f(w)
Для удобства рассмотрим зависимость функции ошибки от одного конкретного веса:

В начальный момент мы находимся в некоторой точке кривой, а для минимизации ошибки попасть мы хотим в точку глобального минимума функции:
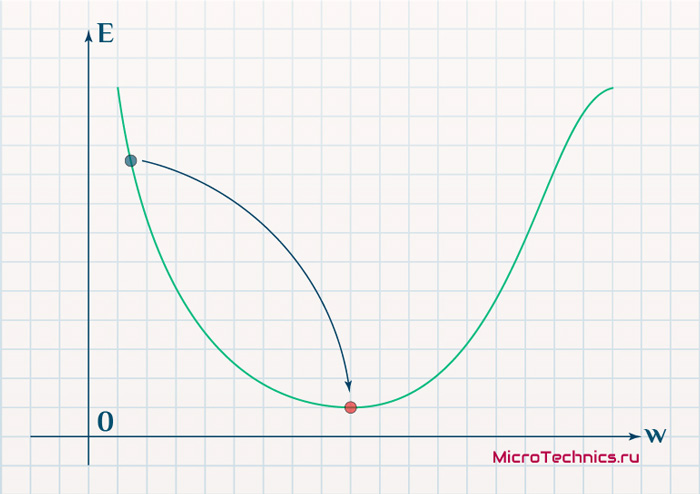
Нанесем на график вектора градиентов в разных точках. Длина векторов численно равна скорости роста функции в данной точке, что в свою очередь соответствует значению производной функции по данной точке. Исходя из этого, делаем вывод, что длина вектора градиента определяется крутизной функции в данной точке:
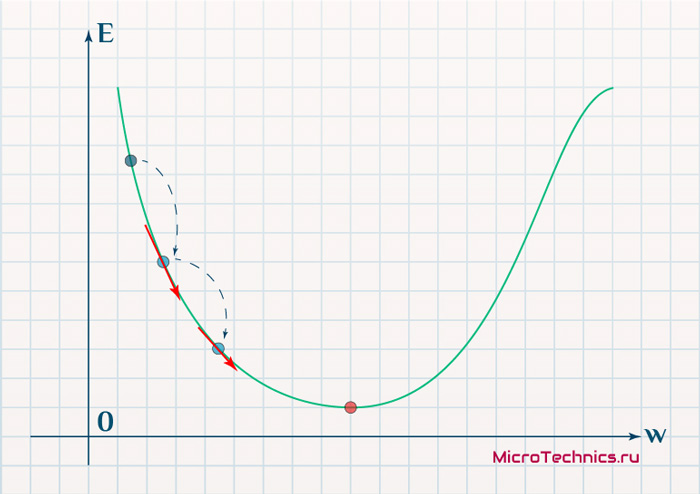
Вывод прост - величина градиента будет уменьшаться по мере приближения к минимуму функции. Это важный вывод, к которому мы еще вернемся. А тем временем разберемся с направлением вектора, для чего рассмотрим еще несколько возможных точек:
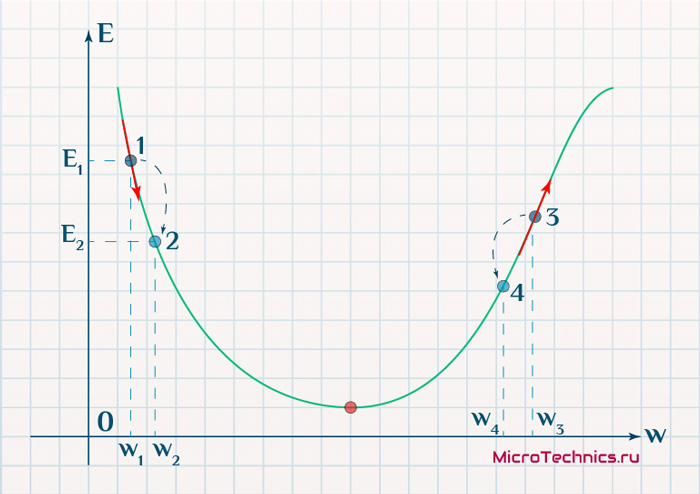
Находясь в точке 1, целью является перейти в точку 2, поскольку в ней значение ошибки меньше (E_2 < E_1), а глобальная задача по-прежнему заключается в ее минимизации. Для этого необходимо изменить величину w на некое значение \Delta w (\Delta w = w_2 - w_1 > 0). При всем при этом в точке 1 градиент отрицательный. Фиксируем данные факты и переходим к точке 3, предположим, что мы находимся именно в ней.
Тогда для уменьшения ошибки наш путь лежит в точку 4, а необходимое изменение значения: \Delta w = w_4 - w_3 < 0. Градиент же в точке 3 положителен. Этот факт также фиксируем.
А теперь соберем воедино эту информацию в виде следующей иллюстрации:
| Переход | \bold{\Delta w} | Знак \bold{\Delta w} | Градиент |
|---|---|---|---|
| 1 \rArr 2 | w_2 - w_1 | + | - |
| 3 \rArr 4 | w_4 - w_3 | - | + |
Вывод напрашивается сам собой - величина, на которую необходимо изменить значение w, в любой точке противоположна по знаку градиенту. И, таким образом, представим эту самую величину в виде:
\Delta w = -\alpha \cdot \frac{dE}{dw}Имеем в наличии:
- \Delta w - величина, на которую необходимо изменить значение w.
- \frac{dE}{dw} - градиент в этой точке.
- \alpha - скорость обучения.
Собственно, логика метода градиентного спуска и заключается в данном математическом выражении, а именно в том, что для минимизации ошибки необходимо изменять w в направлении противоположном градиенту. В контексте нейронных сетей имеем искомый закон для корректировки весов синаптических связей (для синапса между нейронами i и j):
\Delta w_{ij} = -\alpha \cdot \frac{dE}{dw_{ij}}Более того, вспомним о важном свойстве, которое мы отдельно пометили. И заключается оно в том, что величина градиента будет уменьшаться по мере приближения к минимуму функции. Что это нам дает? А то, что в том случае, если наша текущая дислокация далека от места назначения, то величина, корректирующая вес связи, будет больше. А это обеспечит скорейшее приближение к цели. При приближении к целевому пункту, величина \frac{dE}{dw_{ij}} будет уменьшаться, что поможет нам точнее попасть в нужную точку, а кроме того, не позволит нам ее проскочить. Визуализируем вышеописанное:
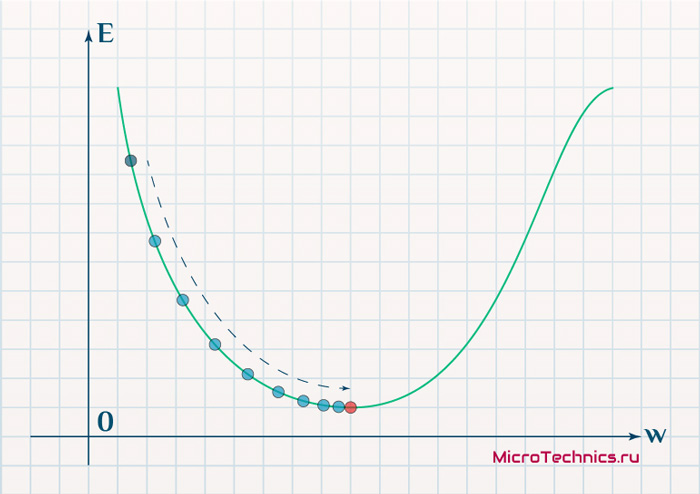
Скорость же обучения несет в себе следующий смысл. Она определяет величину каждого шага при поиске минимума ошибки. Слишком большое значение приводит к тому, что точка может «перепрыгнуть» через нужное значение и оказаться по другую сторону от цели:
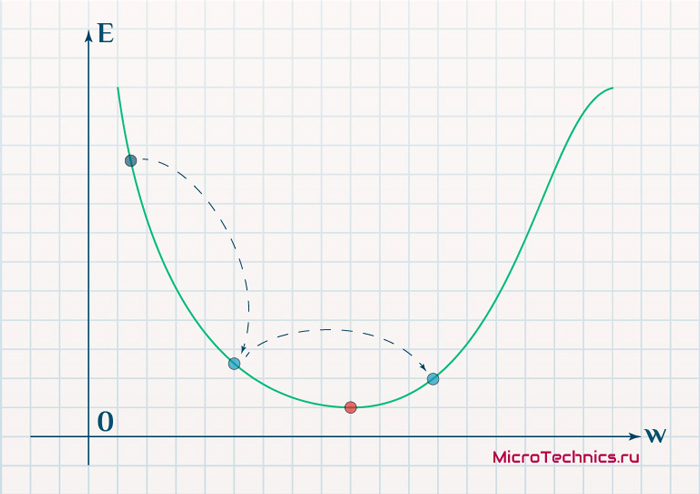
Если же величина будет мала, то это приведет к тому, что спуск будет осуществляться очень медленно, что также является нежелательным эффектом. Поэтому скорость обучения, как и многие другие параметры нейронной сети, является очень важной величиной, для которой нет единственно верного значения. Все снова зависит от конкретного случая и оптимальная величина определяется исключительно исходя из текущих условий.
И даже на этом еще не все, здесь присутствует один важный нюанс, который в большинстве статей опускается, либо вовсе не упоминается. Реальная зависимость может иметь совсем другой вид:
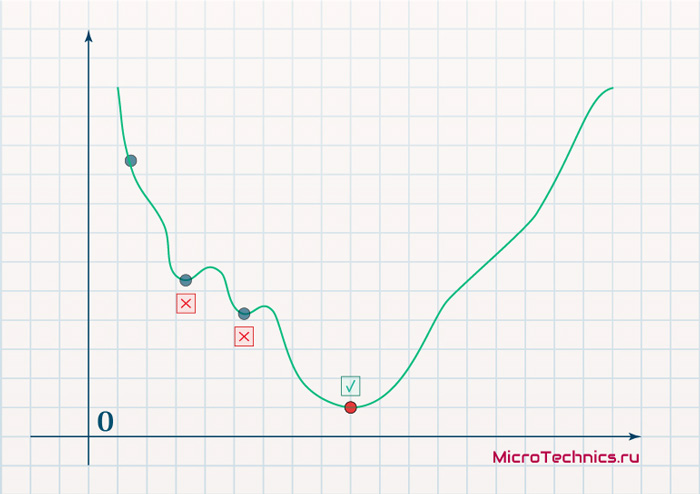
Из чего вытекает потенциальная возможность попадания в локальный минимум, вместо глобального, что является большой проблемой. Для предотвращения данного эффекта вводится понятие момента обучения и формула принимает следующий вид:
\Delta w_{ij} = -\alpha \cdot \frac{dE}{dw_{ij}} + \gamma \cdot \Delta w_{ij}^{t - 1}То есть добавляется второе слагаемое, которое представляет из себя произведение момента на величину корректировки веса на предыдущем шаге.
Итого, резюмируем продвижение к цели:
- Нашей задачей было найти закон, по которому необходимо изменять величину весов связей между нейронами.
- Наш результат - \Delta w_{ij} = -\alpha \cdot \frac{dE}{dw_{ij}} + \gamma \cdot \Delta w_{ij}^{t - 1} - именно то, что и требовалось 👍
И опять же, полученный результат логичным образом перенаправляет нас на следующий этап, ставя вопросы - что из себя представляет функция ошибки, и как определить ее градиент.
Обучение нейронных сетей. Функция ошибки.
Начнем с того, что определимся с тем, что у нас в наличии, для этого вернемся к конкретной нейронной сети. Пусть вид ее таков:
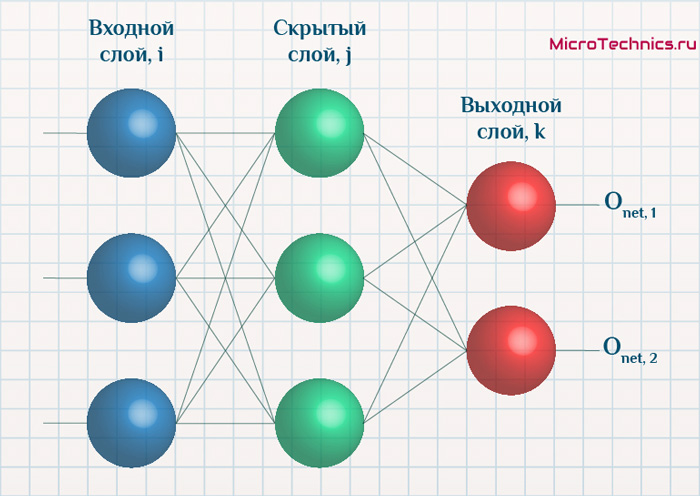
Интересует нас, в первую очередь, часть, относящаяся к нейронам выходного слоя. Подав на вход определенные значения, получаем значения на выходе сети: O_{net, 1} и O_{net, 2}. Кроме того, поскольку мы ведем речь о процессе обучения нейронной сети, то нам известны целевые значения: O_{correct, 1} и O_{correct, 2}. И именно этот набор данных на этом этапе является для нас исходным:
- Известно: O_{net, 1}, O_{net, 2}, O_{correct, 1} и O_{correct, 2}.
- Необходимо определить величины \Delta w_{ij} для корректировки весов, для этого нужно вычислить градиенты (\frac{dE}{dw_{ij}}) для каждого из синапсов.
Полдела сделано - задача четко сформулирована, начинаем деятельность по поиску решения.
В плане того, как определять ошибку, первым и самым очевидным вариантом кажется простая алгебраическая разность. Для каждого из выходных нейронов:
E_k = O_{correct, k} - O_{net, k}Дополним пример числовыми значениями:
| Нейрон | \bold{O_{net}} | \bold{O_{correct}} | \bold{E} |
|---|---|---|---|
| 1 | 0.9 | 0.5 | -0.4 |
| 2 | 0.2 | 0.6 | 0.4 |
Недостатком данного варианта является то, что в том случае, если мы попытаемся просуммировать ошибки нейронов, то получим:
E_{sum} = e_1 + e_2 = -0.4 + 0.4 = 0Что не соответствует действительности (нулевая ошибка, говорит об идеальной работе нейронной сети, по факту оба нейрона дали неверный результат). Так что вариант с разностью откидываем за несостоятельностью.
Вторым, традиционно упоминаемым, методом вычисления ошибки является использование модуля разности:
E_k = | O_{correct, k} - O_{net, k} |Тут в действие вступает уже проблема иного рода:
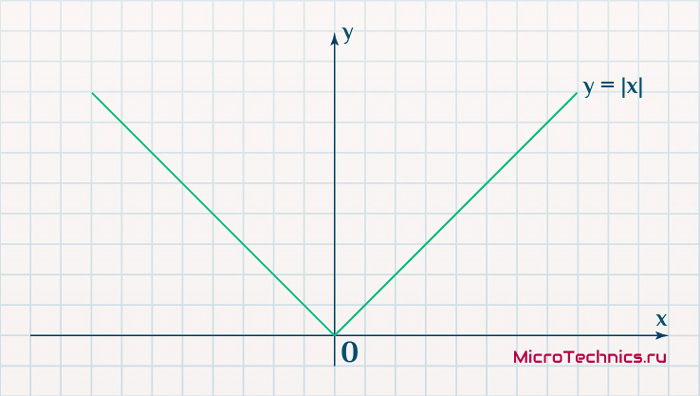
Функция, бесспорно, симпатична, но при приближении к минимуму ее градиент является постоянной величиной, скачкообразно меняясь при переходе через точку минимума. Это нас также не устраивает, поскольку, как мы обсуждали, концепция заключалась в том числе в том, чтобы по мере приближения к минимуму значение градиента уменьшалось.
В итоге хороший результат дает зависимость (для выходного нейрона под номером k):
E_k = \frac{1}{2} \medspace (O_{correct, k} - O_{net, k})^2Множитель 1 / 2 добавлен для удобства дальнейших расчетов, на суть процессов он не влияет, так как по итогу все будет умножаться на произвольно задаваемую скорость обучения.
Функция по многим своим свойствам идеально удовлетворяет нуждам обучения нейронной сети, так что выбор сделан, остановимся на ней. Хотя, как и во многих аспектах, качающихся нейронных сетей, данное решение не является единственно и неоспоримо верным. В каких-то случаях лучше себя могут проявить другие зависимости, возможно, что какой-то вариант даст большую точность, но неоправданно высокие затраты производительности при обучении. В общем, непаханное поле для экспериментов и исследований, это и привлекательно.
Краткий вывод промежуточного шага, на который мы вышли:
- Имеющееся: \frac{dE}{dw_{jk}} = \frac{d}{d w_{jk}}(O_{correct, k} - O_{net, k})^2.
- Искомое по-прежнему: \Delta w_{jk}.
Несложные диффернциально-математические изыскания выводят на следующий результат:
\frac{dE}{d w_{jk}} = -(O_{correct, k} - O_{net, k}) \cdot f{\Large{\prime}}(\sum_{j}w_{jk}O_j) \cdot O_jЗдесь эти самые изыскания я все-таки решил не вставлять, дабы не перегружать статью, которая и так выходит объемной. Но в случае необходимости и интереса, отпишите в комментарии, я добавлю вычисления и закину их под спойлер, как вариант.
Освежим в памяти структуру сети:
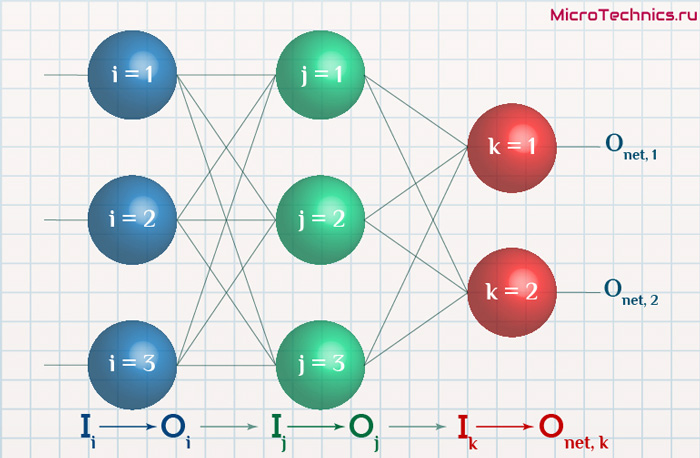
Формулу можно упростить, сгруппировав отдельные ее части:
- (O_{correct, k} - O_{net, k}) \cdot f{\Large{\prime}}(\sum_{j}w_{jk}O_j) - ошибка нейрона k.
- O_j - тут все понятно, выходной сигнал нейрона j.
f{\Large{\prime}}(\sum_{j}w_{jk}O_j) - значение производной функции активации. Причем, обратите внимание, что \sum_{j}w_{jk}O_j - это не что иное, как сигнал на входе нейрона k (I_{k}). Тогда для расчета ошибки выходного нейрона: \delta_k = (O_{correct, k} - O_{net, k}) \cdot f{\Large{\prime}}(I_k).
Итог: \frac{dE}{d w_{jk}} = -\delta_k \cdot O_j.
Одной из причин популярности сигмоидальной функции активности является то, что ее производная очень просто выражается через саму функцию:
f{'}(x) = f(x)\medspace (1\medspace-\medspace f(x))Данные алгебраические вычисления справедливы для корректировки весов между скрытым и выходным слоем, поскольку для расчета ошибки мы используем просто разность между целевым и полученным результатом, умноженную на производную.
Для других слоев будут незначительные изменения, касающиеся исключительно первого множителя в формуле:
\frac{dE}{d w_{ij}} = -\delta_j \cdot O_iКоторый примет следующий вид:
\delta_j = (\sum_{k}{}{\delta_k\medspace w_{jk}}) \cdot f{\Large{\prime}}(I_j)То есть ошибка для элемента слоя j получается путем взвешенного суммирования ошибок, «приходящих» к нему от нейронов следующего слоя и умножения на производную функции активации. В результате:
\frac{dE}{d w_{ij}} = -(\sum_{k}{}{\delta_k\medspace w_{jk}}) \cdot f{\Large{\prime}}(I_j) \cdot O_iСнова подводим промежуточный итог, чтобы иметь максимально полную и структурированную картину происходящего. Вот результаты, полученные нами на двух этапах, которые мы успешно миновали:
- Ошибка:
- выходной слой: \delta_k = (O_{correct, k} - O_{net, k}) \cdot f{\Large{\prime}}(I_k)
- скрытые слои: \delta_j = (\sum_{k}{}{\delta_k\medspace w_{jk}}) \cdot f{\Large{\prime}}(I_j)
- Градиент: \frac{dE}{d w_{ij}} = -\delta_j \cdot O_i
- Корректировка весовых коэффициентов: \Delta w_{ij} = -\alpha \cdot \frac{dE}{dw_{ij}} + \gamma \cdot \Delta w_{ij}^{t - 1}
Преобразуем последнюю формулу:
\Delta w_{ij} = \alpha \cdot \delta_j \cdot O_i + \gamma \cdot \Delta w_{ij}^{t - 1}Из этого мы делаем вывод, что на данный момент у нас есть все, что необходимо для того, чтобы произвести обучение нейронной сети. И героем следующего подраздела будет алгоритм обратного распространения ошибки.
Метод обратного распространения ошибки.
Данный метод является одним из наиболее распространенных и популярных, чем и продиктован его выбор для анализа и разбора. Алгоритм обратного распространения ошибки относится к методам обучение с учителем, что на деле означает необходимость наличия целевых значений в обучающих сетах.
Суть же метода подразумевает наличие двух этапов:
- Прямой проход - входные сигналы двигаются в прямом направлении, в результате чего мы получаем выходной сигнал, из которого в дальнейшем рассчитываем значение ошибки.
- Обратный проход - обратное распространение ошибки - величина ошибки двигается в обратном направлении, в результате происходит корректировка весовых коэффициентов связей сети.
Начальные значения весов (перед обучением) задаются случайными, есть ряд методик для выбора этих значений, я опишу в отдельном материале максимально подробно. Пока вот можно полистать - ссылка.
Вернемся к конкретному примеру для явной демонстрации этих принципов:
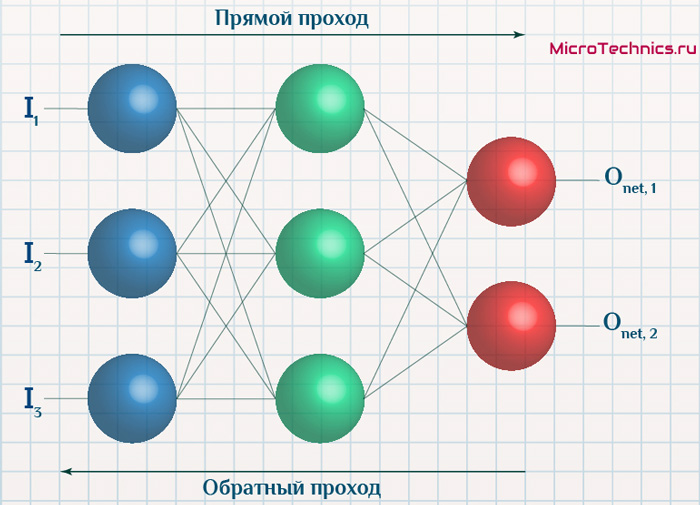
Итак, имеется нейронная сеть, также имеется набор данных обучающей выборки. Как уже обсудили в начале статьи - обучающая выборка представляет из себя набор образцов (сетов), каждый из которых состоит из значений входных сигналов и соответствующих им «правильных» значений выходных величин.
Процесс обучения нейронной сети для алгоритма обратного распространения ошибки будет таким:
- Прямой проход. Подаем на вход значения I_1, I_2, I_3 из обучающей выборки. В результате работы сети получаем выходные значения O_{net, 1}, O_{net, 2}. Этому целиком и полностью был посвящен предыдущий манускрипт.
- Рассчитываем величины ошибок для всех слоев:
- для выходного: \delta_k = (O_{correct, k} - O_{net, k}) \cdot f{\Large{\prime}}(I_k)
- для скрытых: \delta_j = (\sum_{k}{}{\delta_k\medspace w_{jk}}) \cdot f{\Large{\prime}}(I_j)
- Далее используем полученные значения для расчета \Delta w_{ij} = \alpha \cdot \delta_j \cdot O_i + \gamma \cdot \Delta w_{ij}^{t - 1}
- И финишируем, рассчитывая новые значения весов: w_{ij \medspace new} = w_{ij} + \Delta w_{ij}
- На этом один цикл обучения закончен, данные шаги 1 - 4 повторяются для других образцов из обучающей выборки.
Обратный проход завершен, а вместе с ним и одна итерация процесса обучения нейронной сети по данному методу. Собственно, обучение в целом заключается в многократном повторении этих шагов для разных образцов из обучающей выборки. Логику мы полностью разобрали, при повторном проведении операций она остается в точности такой же.
Таким образом, максимально подробно концентрируясь именно на сути и логике процессов, мы в деталях разобрали метод обратного распространения ошибки. Поэтому переходим к завершающей части статьи, в которой разберем практический пример, произведя полностью все вычисления для конкретных числовых величин. Все в рамках продвигаемой мной концепции, что любая теоретическая информация на порядок лучше может быть осознана при применении ее на практике.
Пример расчетов для метода обратного распространения ошибки.
Возьмем нейронную сеть и зададим начальные значения весов:
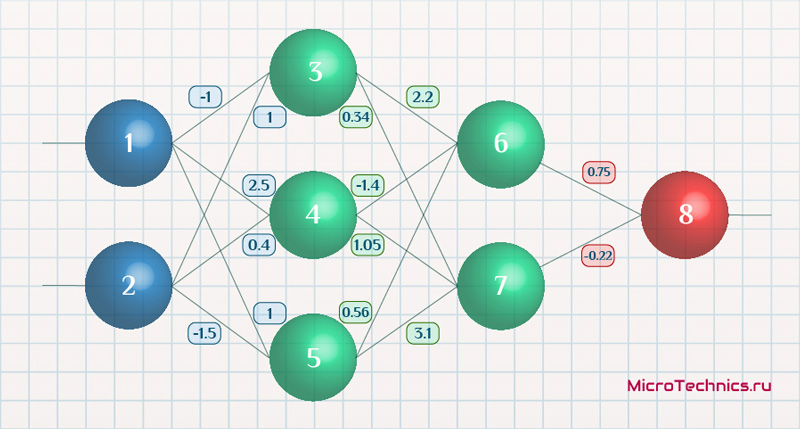
Здесь я задал значения не в соответствии с существующими на сегодняшний день методами, а просто случайным образом для наглядности примера.
В качестве функции активации используем сигмоиду:
f(x) = \frac{1}{1 + e^{-x}}И ее производная:
f{\Large{\prime}}(x) = f(x)\medspace (1\medspace-\medspace f(x))Берем один образец из обучающей выборки, пусть будут такие значения:
- Входные: I_1 = 0.6, I_1 = 0.7.
- Выходное: O_{correct} = 0.9.
Скорость обучения \alpha пусть будет равна 0.3, момент - \gamma = 0.1. Все готово, теперь проведем полный цикл для метода обратного распространения ошибки, то есть прямой проход и обратный.
Прямой проход.
Начинаем с выходных значений нейронов 1 и 2, поскольку они являются входными, то:
O_1 = I_1 = 0.6 \\ O_2 = I_2 = 0.7
Значения на входе нейронов 3, 4 и 5:
I_3 = O_1 \cdot w_{13} + O_2 \cdot w_{23} = 0.6 \cdot (-1\medspace) + 0.7 \cdot 1 = 0.1 \\
I_4 = 0.6 \cdot 2.5 + 0.7 \cdot 0.4 = 1.78 \\
I_5 = 0.6 \cdot 1 + 0.7 \cdot (-1.5\medspace) = -0.45На выходе этих же нейронов первого скрытого слоя:
O_3 = f(I3\medspace) = 0.52 \\ O_4 = 0.86\\ O_5 = 0.39
Продолжаем аналогично для следующего скрытого слоя:
I_6 = O_3 \cdot w_{36} + O_4 \cdot w_{46} + O_5 \cdot w_{56} = 0.52 \cdot 2.2 + 0.86 \cdot (-1.4\medspace) + 0.39 \cdot 0.56 = 0.158 \\
I_7 = 0.52 \cdot 0.34 + 0.86 \cdot 1.05 + 0.39 \cdot 3.1 = 2.288 \\
O_6 = f(I_6) = 0.54 \\
O_7 = 0.908Добрались до выходного нейрона:
I_8 = O_6 \cdot w_{68} + O_7 \cdot w_{78} = 0.54 \cdot 0.75 + 0.908 \cdot (-0.22\medspace) = 0.205 \\
O_8 = O_{net} = f(I_8) = 0.551Получили значение на выходе сети, кроме того, у нас есть целевое значение O_{correct} = 0.9. То есть все, что необходимо для обратного прохода, имеется.
Обратный проход.
Как мы и обсуждали, первым этапом будет вычисление ошибок всех нейронов, действуем:
\delta_8 = (O_{correct} - O_{net}) \cdot f{\Large{\prime}}(I_8) = (O_{correct} - O_{net}) \cdot f(I_8) \cdot (1-f(I_8)) = (0.9 - 0.551\medspace) \cdot 0.551 \cdot (1-0.551\medspace) = 0.0863 \\
\delta_7 = (\sum_{k}{}{\delta_k\medspace w_{jk}}) \cdot f{\Large{\prime}}(I_7) = (\delta_8 \cdot w_{78}) \cdot f{\Large{\prime}}(I_7) = 0.0863 \cdot (-0.22\medspace) \cdot 0.908 \cdot (1 - 0.908\medspace) = -0.0016 \\
\delta_6 = 0.086 \cdot 0.75 \cdot 0.54 \cdot (1 - 0.54\medspace) = 0.016 \\
\delta_5 = (\sum_{k}{}{\delta_k\medspace w_{jk}}) \cdot f{\Large{\prime}}(I_5) = (\delta_7 \cdot w_{57} + \delta_6 \cdot w_{56}) \cdot f{\Large{\prime}}(I_7) = (-0.0016 \cdot 3.1 + 0.016 \cdot 0.56) \cdot 0.39 \cdot (1 - 0.39\medspace) = 0.001 \\
\delta_4 = (-0.0016 \cdot 1.05 + 0.016 \cdot (-1.4)) \cdot 0.86 \cdot (1 - 0.86\medspace) = -0.003 \\
\delta_3 = (-0.0016 \cdot 0.34 + 0.016 \cdot 2.2) \cdot 0.52 \cdot (1 - 0.52\medspace) = 0.0087С расчетом ошибок закончили, следующий этап - расчет корректировочных величин для весов всех связей. Для этого мы вывели формулу:
\Delta w_{ij} = \alpha \cdot \delta_j \cdot O_i + \gamma \cdot \Delta w_{ij}^{t - 1}Как вы помните, \Delta w_{ij}^{t - 1} - это величина поправки для данного веса на предыдущей итерации. Но поскольку у нас это первый проход, то данное значение будет нулевым, соответственно, в данном случае второе слагаемое отпадает. Но забывать о нем нельзя. Продолжаем калькулировать:
\Delta w_{78} = \alpha \cdot \delta_8 \cdot O_7 = 0.3 \cdot 0.0863 \cdot 0.908 = 0.0235 \\
\Delta w_{68} = 0.3 \cdot 0.0863 \cdot 0.54= 0.014 \\
\Delta w_{57} = \alpha \cdot \delta_7 \cdot O_5 = 0.3 \cdot (−0.0016\medspace) \cdot 0.39= -0.00019 \\
\Delta w_{47} = 0.3 \cdot (−0.0016\medspace) \cdot 0.86= -0.0004 \\
\Delta w_{37} = 0.3 \cdot (−0.0016\medspace) \cdot 0.52= -0.00025 \\
\Delta w_{56} = \alpha \cdot \delta_6 \cdot O_5 = 0.3 \cdot 0.016 \cdot 0.39= 0.0019 \\
\Delta w_{46} = 0.3 \cdot 0.016 \cdot 0.86= 0.0041 \\
\Delta w_{36} = 0.3 \cdot 0.016 \cdot 0.52= 0.0025 \\
\Delta w_{25} = \alpha \cdot \delta_5 \cdot O_2 = 0.3 \cdot 0.001 \cdot 0.7= 0.00021 \\
\Delta w_{15} = 0.3 \cdot 0.001 \cdot 0.6= 0.00018 \\
\Delta w_{24} = \alpha \cdot \delta_4 \cdot O_2 = 0.3 \cdot (-0.003\medspace) \cdot 0.7= -0.00063 \\
\Delta w_{14} = 0.3 \cdot (-0.003\medspace) \cdot 0.6= -0.00054 \\
\Delta w_{23} = \alpha \cdot \delta_3 \cdot O_2 = 0.3 \cdot 0.0087\medspace \cdot 0.7= 0.00183 \\
\Delta w_{13} = 0.3 \cdot 0.0087\medspace \cdot 0.6= 0.00157И самый что ни на есть заключительный этап - непосредственно изменение значений весовых коэффициентов:
w_{78 \medspace new} = w_{78} + \Delta w_{78} = -0.22 + 0.0235 = -0.1965 \\
w_{68 \medspace new} = 0.75+ 0.014 = 0.764 \\
w_{57 \medspace new} = 3.1 + (−0.00019\medspace) = 3.0998\\
w_{47 \medspace new} = 1.05 + (−0.0004\medspace) = 1.0496\\
w_{37 \medspace new} = 0.34 + (−0.00025\medspace) = 0.3398\\
w_{56 \medspace new} = 0.56 + 0.0019 = 0.5619 \\
w_{46 \medspace new} = -1.4 + 0.0041 = -1.3959 \\
w_{36 \medspace new} = 2.2 + 0.0025 = 2.2025 \\
w_{25 \medspace new} = -1.5 + 0.00021 = -1.4998 \\
w_{15 \medspace new} = 1 + 0.00018 = 1.00018 \\
w_{24 \medspace new} = 0.4 + (−0.00063\medspace) = 0.39937 \\
w_{14 \medspace new} = 2.5 + (−0.00054\medspace) = 2.49946 \\
w_{23 \medspace new} = 1 + 0.00183\medspace = 1.00183 \\
w_{13 \medspace new} = -1 + 0.00157\medspace = 0.99843\\И на этом данную масштабную статью завершаем, конечно же, не завершая на этом деятельность по использованию нейронных сетей. Так что всем спасибо за прочтение, любые вопросы пишите в комментариях и на форуме, ну и обязательно следите за обновлениями и новыми материалами, до встречи!










Спасибо! Следим! Ну и ждем интересный пример из собственных задач и программную реализацию на QT 🙂
Теория и математика очень круто 🙂 А как использовать на практике в Embedded? например на STM32 или BeagleBone, Black Raspberry Pi
Я, честно говоря, не уверен, что STM32, например, потянет сложные задачи на ИНС )
Очень интересно, напишите примеры где можно использовать ИИ
В основном задачи классификации, распознавания образцов. Кроме того, задачи прогнозирования.
пожалуй,единственная статья(+предыдущая),которая мне действительно помогла в понимании нейросетей.
спасибо автор!
сейчас борюсь с дипломом...много вопросов...
Очень сильно поможет, если вы приведете код
Я хоть и понимаю формулы, но как-то на родном си будет гораздо легче и понятней
Может я ошибаюсь, но комбинированный ввод элементов 2,3 и 4 рассчитаны в примере как 0.8 , 0.7 и -0.4 соответственно, и при этом их активности указаны как 0.31, 0.33 и 0.60 однако если в функцию активации подставить значения 0.8 , 0.7 и -0.4 то результаты будут 0.69, 0.67 и 0.40 соответственно. Вопрос как появились значения 0.31, 0,33 и 0,60 ?
P.S. Очевидно что 0.31 = 1- 0.69 и т.д
Эх...Спасибо большое за замечание, видимо когда-то при написании статьи при расчетах был потерян знак минус в степени экспоненты..Сейчас исправлю все числовые значения, еще раз спасибо
по моему та же ошибка осталась для 5-го элемента:
при 3.63 функция активации должна быть 0,974
Да, все верно
Статья очень понравилась, единственное не могу до сих пор вкурить что обозначает (вычисляет) данная формула
f'(net_j)=f(net_j)*(1-f(net_j))
Объясните пожалуйста.
Это производная функции f(net_j), если рассчитать производную, то получится выражение, которое можно выразить через исходную функцию.
>Здесь значения 0.009, 0.018 и 0.036 получаются в результате прохода ошибки выходного элемента 0.009 по взвешенным связям в направлении к элементам 2, 3 и 4 соответственно.
наверное, имелось ввиду
Здесь значения -0.014, -0.028 и -0.056 получаются в результате прохода ошибки выходного элемента -0.014 по взвешенным связям в направлении к элементам 2, 3 и 4 соответственно.
Да, спасибо, поправлю
спасибо за статью. простой счет в ручном режиме действительно вправляет понимание процедуры, в других местах от формул в статьях пухнет голова, тем более, что авторы, судя по всему, сами не всегда до конца понимают, как алгоритм реально работает.
не вижу только в статье, откуда взялась формула для вычисления ошибки на выходном слое δ5 как
δ5 = (y0-y)*f(net5)(1-f(net5)) [1]
после которой получилось δ5=-0.014
если следовать формуле для вычисления δj по δk
δj=f(net-j)*(1-f(net-j))*Σwk*δk [2]
то для того, чтобы для δ5 получилась формула [1] из формулы [2], нужно взять j=5, k=6: получается, что типа добавляем фиктивный выход 6 с входным нейроном 5 с весом w6=1 и ошибкой δ6=y0-y
другой вариант - просто постулировать формулу [1] для вычисления ошибки выходного слоя
третий вариант - брать ошибку для выходного слоя δ5=(y0-y), как показано в начале статьи, но в таком случае вычисления в статье не верны
Добрый день!
В формуле [2] часть, которая находится под знаком суммы представляет из себя ошибку на выходе нейрона j, а для выходного нейрона получается, что эту ошибку мы знаем уже из самого условия задачи, ведь стоит цель получить определенное значение на выходе сети. Поэтому, по большому, счету можно считать, что мы добавляем "виртуальный" элемент с весом 1, он и даст как раз такую же ошибку выходного нейрона.
Написал реализацию сетки с обучением на Java, взял δ5 = (y0-y), все работает, думаю, нюанс не принципиальный, пойдут оба варианта.
Такой вопрос. Прогоняю обучение для одного набора входных параметров - все отлично, на две-три итерации получаю желаемый вывод с нужной точностью. Загоняю пример для другой комбинации входов, все тоже хорошо, сетка снова обучается, но при этом, очевидно, затираются значения весов, полученные на первой итерации обучения, результат для первой комбинации входных параметров получается неправильный.
Пробую учить простому XOR, два входа, два скрытых нейрона, один выход.
Сам алгоритм распространения ошибки, понятно, работает, но можно ли с ним как-то обучать сетку воспринимать одновременно множественные варианты входных параметров?
(y0-y) - это ошибка именно выхода 5 элемента, а нам нужно ее как бы провести через 5 элемент обратно, поэтому нужно умножать на другие множители.
Огромное спасибо за статью. Теперь алгоритм полностью понятен, но если повторять данную процедуру обучения сети из примера, то выход сети будет равен всегда единице и соответственно сеть перестаёт обучаться и просто зацикливается. Если вам не трудно, то помогите пожалуйста. Было бы замечательно увидеть реализацию данного алгоритма на языке c++ или любом другом языке.
Ну эта сеть просто для примера одного прохода цикла обучения. В реальной задаче нужно огромное количество наборов данных (желаемый выход при разных значениях входов). И плюс для реальной сети важно подобрать оптимальное количество нейронов и слоев.
А есть возможность связаться с вами в соц. сети и пообщаться на тему нейронных сетей? Был бы очень благодарен.
Да, конечно, вот группа сайта - https://vk.com/microtechnics, можно там, ну и там есть на мою страницу ссылка, можно просто через сообщения )
А можете пример привести пример для 3-4 слойной сети. Реально корректировка весов за з-слоем вводит в ступор
Добрый день!
Добавил в конце статьи описание небольшое.
5. Определяем ошибки элементов первого скрытого слоя (0 и 1):
Насколько я понял во второй формуле должна быть f(net1)
Да, все верно, большое спасибо, исправил.
Добрый день! Спасибо за статью!
Боюсь показаться чайником, но возник интересный вопрос? Подскажите пожалуйста как можно определить выходные условия если они не известны? Есть ли для этого методики? Например для распознавания определенного символа (буквы, цифры) с картинки.
Добрый день!
Сети все равно нужно предъявить известные образцы во время обучения, чтобы в дальнейшем она могла распознавать и неизвестные.
Похоже ошибки в формулах с дельта. W_(k, j) - это вес из k в j. А на примерах вы берете как раз-таки все дельты, В КОТОРЫЕ входят стрелочки. Короче говоря, в формулах для дельта должно быть не w(k, j), а w(j, k). Не так ли?
Добрый день!
Вес связи между нейронами - это просто значение, не векторная величина, то есть по сути нет разницы: w(1, 2) = w(2,1). Но для улучшения восприятия Ваш вариант мне нравится больше, изменю в статье.
Спасибо за замечание!
Здравствуйте, правильно ли я понимаю, что если у нас теперь есть новые весовые коэффициенты, то учитывая их , выход сети должен быть равен - 0,4 ? Или мы должны еще по много раз находить новые весовые коэффициенты, до тех пор пока выход сети не станет равным - 0,4 ?
Добрый вечер!
Если в целом, то у нас должно быть много таких комбинаций значений (значений входов и соответствующих им значений выходов), и мы прогоняем эти данные через сеть много раз до тех пор, пока результаты работы сети не станут удовлетворительными.
Ну например, я всегда буду на вход подавать только 0.2 и 0.5 и ждать с выхода сети 0,4. Получается за один проход, не получится 0,4 получить ? Нужно как вы говорите много раз пройти корректировку весов ?
Да, за один проход не получится.
Здравствуйте. Я сделал на Си нейронную сеть, там у меня просто 1 входной элемент, 1 скрытый, 1 выходной. Она находит ожидаемый выход, но не для всех входных значений и не для всех начальных весовых коэффициентов. Правильно ли я понимаю, что начальные весовые коэффициенты должны быть какими то определенными ? И еще вопрос, есть ли смысл от такой маленькой сети которую я сделал или лучше сразу начинать с двумя входами, 2 скрытыми и 1 выходным элементами ?
Добрый день!
Вообще тут нет четких правил - для каждого применения все индивидуально подбирается в ходе экспериментов. Количество входов и выходов зависит от цели. Если к примеру у нас функция двух переменных f(x, y), и мы хотим обучить сеть этой функции, то, соответственно, будет два входа и один выход.
А веса чаще всего инициализируются небольшими случайными значениями - от -0.5 до 0.5, например.
Спасибо!
Обращайтесь, если что, постараюсь помочь)
Здравствуйте! У вас нет примера того как обучить сеть получать один и тот же выходной сигнал, при разных парах входных значениях? То есть первый раз мы кинули на вход (0.2 и 0.5) получили выход сети — 0.4. Можно ли на вход бросить например (0,3 и 0,8) и получить тоже 0,4 ?
Добрый вечер!
К сожалению, практической реализации нет сейчас... Но тут точно такие же принципы, не важно, что на выходе одинаковое значение, все должно работать.
Добрый день! Спасибо за статью. Но, к Вам есть вопрос! Если истинный выход сети меняется, как поступать? К примеру, у нас имеется таблица XOR и в зависимости от входных X и Y результат операции будет либо нуль, либо единица. Как научить нейросеть угадывать результат XOR? Заранее большое спасибо!
Добрый день!
У нас тогда получается есть несколько наборов данных - (вход, вход, выход). И мы все эти данные по очереди многократно прогоняем по алгоритму обратного распространения.
Спасибо за быстрый ответ! Я Вам уже успел на эмэйл написать =) Извиняюсь. Не могли бы Вы еще объяснить что значит (вход, вход, выход)? Я прогоняю X и Y (1; 1), (1; 0), (0; 1), (0; 0) вместо Ваших указанных (в статье) 0.2 и 0.5. Что я делаю неверно?
Вы также мне поможете, если объясните как можно научить сеть предугадывать функцию y = x ^ 2.
В примере у нас есть такой образец для обучения:
Вход 1: 0.2, Вход 2: 0.5, Выход: 0.4.
Для XOR будут такие образцы:
Вход 1: 0, Вход 2: 0, Выход: 0.
Вход 1: 0, Вход 2: 1, Выход: 1.
Вход 1: 1, Вход 2: 0, Выход: 1.
Вход 1: 1, Вход 2: 1, Выход: 0.
И по такому же принципу как в примере работаем.
Для y = x^2 нужно какое-то количество значений использовать для обучения, например:
Вход 1: 1, Выход: 1.
Вход 1: 2, Выход: 4.
Вход 1: 3, Выход: 9.
Вход 1: 4, Выход: 16.
Вход 1: 5, Выход: 25.
Прогоняем эту обучающую последовательность через сеть, и затем после подачи на вход сети других значений сеть сможет выдать правильный результат.
Спасибо огромное! Разъяснили. В случае с XOR, выходит что сеть обучится за четыре итерации?
Нет, нужно будет много раз эти 4 образца ей передавать, пока результат не станет удовлетворительным.
И с квадратичной функцией так же - много раз прогоняем какое-то количество данных по кругу, затем можно тестировать на других данных, которые в обучении не принимали участия.
Последний вопрос и оставлю Вас в покое. Во время тестирования некоторые веса повышаются аж до 2. Это нормально?
Спрашивайте сколько угодно =)
2 - вполне нормальная величина. Возможна ситуация, когда веса будут до бесконечности увеличиваться, тогда нужно будет норму обучения уменьшить, либо другие меры принять. Но это уже в процессе тестирования будет понятно.
Спасибо еще раз Вам большое за помощь. Вы принесли свет знаний в мою жизнь, хех. Я не премину такой возможностью и в случае чего задам еще парочку глупых вопросов. А пока что, пойду опробую все, что Вы мне посоветовали. Действительно очень помогли. Хорошего дня 🙂
Спасибо, удачи )
Вечер добрый! Еще один вопрос, вечерний. Так вот, если обучать систему операции XOR, то выходит, что контрольные значения следует подменять вместе с входными (т.е., что контрольные значения, те, которые достоверные, соответствовали входным). Я все правильно понимаю? Но, как тогда понимать, что обучение закончено успешно? Заранее спасибо.
Да, каждый обучающий образец состоит из входных значений и выходных, которые соответствуют этим входным. А успешность обучения можно определять по результату прямого прохода.
Т.е., ничего особенного добавлять в алгоритм не следует? Ведь я использую Ваш пример. Еще раз спасибо
Да, это общий алгоритм для обучения сетей такого вида. Само собой, для каждой конкретной задачи меняется структура сети, количество элементов и т д.
Добрый вечер! Вы не могли бы помочь или наставить советом? Столкнулся со следующей проблемой. У меня есть нейронная сеть с обратным распространением ошибок. При обучении сети выдавать одно и тоже число, вне зависимости от значения входных параметров (как у Вас в статье), все проходит отлично, и она справляется с задачей. Но! Как только я пытаюсь добавить еще одну пару параметров к примеру: 0.2, 0.3 соответствует 0.8 (все идет хорошо), а вот, 0.2, 0.3 соответствует 0.8; 0.4, 0.6 cсоответствует 0.5 -- уже не работает. Т.е., когда у нейросети более одного контрольного параметра она не справляется с задачей. Такое ощущение, будто подстроив веса к первому контрольному параметру, она сразу теряет полученный результат, подстроив ко второму параметру. Как быть? Заранее спасибо
Моя нейросеть состоит из двух входов, трех нейронов в скрытом слое и одного выхода.
Добрый день!
Для любой похожей задачи, в целом, обычно примерно одинаковые действия - подбирать начальные значения весов, норму обучения, вид сети (хотя я думаю Ваш вариант 2-3-1 вполне подходит). И, конечно, если это программная реализация, то перепроверить алгоритмы, чаще всего находится какая-нибудь небольшая ошибка, которая мешает сети обучиться.
Спасибо! Вы были правы, я нашел ошибку
Хорошо =)
Спасибо огромное. Именно таких примеров "на пальцах", посчитанных ручками я и искал долгое время. Наконец получилось создать нейросеть на Питоне. Пока только с одним скрытым слоем. Работает великолепно!!! Причём написал код так, что можно изменять до бесконечности количество входных нейронов и нейронов скрытого слоя.
Теперь буду писать код для нескольких скрытых слоёв с сохранением парадигмы расширяемости количества нейронов в слоях.
Ещё раз огромное спасибо! Мастер!!!
Большое спасибо за отличные слова! =)
Рад, что статья оказалась полезной!
Спасибо! Отличная и наглядная практическая статья) Первая по которой не только удалось сделать свою реализацию НС но понять что есть что и для чего) Грамотно расставила всё по полочка в голове)
У меня есть вопрос:
Начинаю со случайных весов и обучаю НС XOR'у
В большинстве обучений всё в порядке и НС выдаёт ожидаемый результат, например:
[0,1] => 0.99; [1,0] => 0.97; [0,0] => 0.00; [1,1] => 0.02
Но иногда после обучения НС выдаёт странный результат, например:
[0,1] => 0.99; [1,0] => 0.99; [0,0] => 6.52; [1,1] => 0.00
Один из выходных результатов куда то "уплывает" независимо от количества итераций обучения.
В чём может быть проблема?
Спасибо, рад, что статья понравилась! =)
А какие значению весов получаются в "правильном" случае и когда результат уплывает?
Спасибо большое за статью, наконец-то нашёл пример того, что происходит в ИНС!
Интересно, много ли математики скрыто от нас в том месте статьи, где даны итоговые формулы расчёта ошибки и активности элемента? Хотя, возможно, их можно и как данность принять, т.к. в целом механизм понятен. Было бы здорово, если бы мат.аппарат все же приводился, но был как-то выделен - мол, если сложно, пропускай этот кусок, читай дальше, но ты всё поймешь 🙂
И несколько вопросов, связанных с пониманием. Я моделирую в Матлабе нейронные сети для прогнозирования. Если не фиксировать начальные условия при обучении, то результат обучения ИНС каждый раз отличается - сеть может работать чуть лучше, или чуть хуже. Насколько я понимаю, в Матлабе по умолчанию заданы параметры, при которых обучение останавливается, если пересчёт весов не приводит к улучшению в работе сети.
1) Верно ли, что такой момент остановки может возникнуть до того момента, как кончится обучающая выборка? Если да, то Матлаб просто не задействует оставшиеся данные при обучении, или использует их для валидации/тестирования?
2) Если положим, что число допустимых итераций бесконечно, и обучающая выборка также бесконечна, не должна ли ИНС теоретически приходить к одним и тем же настройкам весов при разных начальных весах, выставленных произвольно? Учитывая, что начальные веса, как указано в статье, берутся из небольшого диапазона [-0.5,0.5], то вообще, кажется, что и при весьма ограниченной выборке ИНС должна быстро прийти к одной и той же конфигурации (правда, я так понял, этого не происходит).
2) Выборку в Матлабе можно разбить на Training, Validation и Testing. Не совсем понимаю, что это за этап - Validation и для чего он нужен?
Заранее спасибо!
Добрый день!
Хорошая идея с блоком для математических выкладок, который можно скрывать, спасибо!
Да, если обучающая выборка избыточна, то в какой-то момент обучение остановится, до окончания выборки. Например, нужно обучить сеть функции y(x) = 2 * x. Можно подавать ей бесконечное количество образцов для обучения, но на практике десятка-другого (навскидку) набора данных будет уже достаточно.
И по поводу второго вопроса - примерно аналогичная ситуация. Если задача довольно проста, то теоретически может получиться так, что две нейронные сети с разными весами смогут одинаково хорошо ее решать. То есть в этом случае в процессе обучения могут получиться разные веса при разных начальных условиях. Но в целом, в большинстве задач, результат обучения не должен зависеть от выбранных весов. Все очень сильно зависит от конкретного случая, от задачи, данных, конфигурации сети...
Вот по поводу Матлаба ничего, к сожалению, не могу сказать, не пользуюсь...
Здравствуйте. Очень круто! Стало понятно, как выполняются расчеты. И все-атки, уменя вопрос - как определять число нейронов в скрытом слое? Почему в примере 1 у нас 3 нейрона, а не 2 или 4?
Добрый день!
На самом деле конкретного правила или формулы нет... Все определяется экспериментально для каждой конкретной задачи. Один из вариантов - начинать с малого числа нейронов. То есть задать 1-2 нейрона в скрытом слое, провести обучение, по результатам уже смотреть. "1-2 нейрона" - это тоже цифра, зависящая от задачи, если нужно обрабатывать огромное количество данных и параметров, нет смысла начинать с 1-го нейрона и увеличивать до 2-х, 3-х и т. д.
Привет! В чем разница умножать дифференциал сигмойды сразу на ошибку, как в вашем методе и потом при коррекции весов? попробовал оба метода, результаты разные выдает, еще видел метод с коррекцией весов сразу (если есть возможность, то и это метод просьба показать). Еще заметил, что при разных начальных значений весов сеть может не сходиться( Сначала думал, что ошибка в коде, но все верно.
Добрый день!
Ну если математически эквивалентно получается, если умножать в другом месте, то результат меняться не должен.
А сильно начальные значения отличаются, когда сходится и когда нет? Но вообще, в целом, такое вполне может быть.
Добрый!
1) а математически эти методы одинаковы?
2) рендом от -0,5 до 0,5 выставил, но сокрость также влияет. и это на сети 2-2-1. т.е. нужно еще постараться, чтобы она сошлась. реально странно или все-таки это нормально даже для таких простых сетей? (
3) еще вопрос какой физический смысл в скрытых слоях? как я понял в линейно-разделимых задачах они, вообще, не нужны? и они влияют только на нелинейные, но как?
А можете уточнить, какие именно методы =)
Все очень сильно зависит от конкретной задачи, может обучающая выборка недостаточно большая...
Однослойный перцептрон может решить задачу только если данные линейно разделимы, для более сложных задач уже нужен как минимум 1 скрытый слой.
1) статья на хабре https://habr.com/ru/post/313216/ и изветсная гифка в середине. там умножают дифф после вычилсения всех ошибок.
2) 4 элемента. XOR задача. могу код скинуть, если нужно. на javascript писал с графиком)
3) как я понимаю, чем больше и сложнее взаимных пересечений, тем больше нужно скрытых слоев?
4) изучал движения прямой в 2-1 и обратил внимание, что не всегда прямая движется соазу к правильному углу, а переварачивается и заходит с другой стороны O.o Так должно быть?)
вот пример (синия - начало, красная - конец, зеленая - 5 эпоха):
Добрый вечер!
Может дело в позднем времени, но я что-то отличий в методе не обнаружил на хабре...
Если пришлете, могу посмотреть код, по мере возможности, может ближе к выходным, если не получится завтра. Свежий взгляд со стороны и все такое )
В теории да, чем сложнее задача, тем больше скрытых слоев. Но в теории нейронных сетей все очень индивидуально (зависит от задачи, данных и т. д.), поэтому сложно поддается каким-то единым правилам. Вот, к примеру, есть такое мнение, что "если задачу не получается решить с одним скрытым слоем, то значит эта задача не подходит для этой сети, в принципе"... Но это, конечно, спорно )
ну там сначала вычисляют все ошибки и только, когда производят коррекцию весов умножают на дифференциал, у вас же находят ошибку и сразу умножают на дифферинциал. т.е. в вашем методе первый дифференциал и последующие протаскиваются через всю сеть, т.к. ошибки зависят друг от друга, а там только точечно для каждого веса. дифференциал тут не влиятет на всю сеть. вопрос, что лучше?
чет там хостинг картинок не пашет, вот новая фотка к 4 вопросу:
Давайте по той статье по частям, на каком этапе отличие?
1. Находим ошибку выходного нейрона О1.
2. Ошибка Н1.
3. Изменение веса W5.
4. Повторяем для H2, W6.
5. Дальше ошибки и корректировки весов для I1 и I2.
По поводу графика мне кажется, что это нормальное явление...)
3. Изменяем веса путем умножения еще диффиренциала
я проверял оба метода. результаты разные получается.
залил на гитхаб)
2-2-1
https://github.com/Listian/neuro_test
Вот этот вариант верный:
Вопрос в том, что и на хабре так же сделано )
δO1 = (1 — 0.33) * ( (1 — 0.33) * 0.33 ) = 0.148
(1 - 0.33) эквивалентно в данном случае (item['out']['1'] - out3;), сразу умножается на производную.
ок. я просто сделал по двум методам и результаты разные получились, п.э. возникли вопросы, т.к. я не математик)
тем более мне все равно ваш метод больше нравится, т.к. он проще в реализации и нагляднее, когда в циклах все будет уже, на каждом этапе свое минимальное действие происходит)
другой метод муторнее намного.
🙂
Интересен вопрос пригодности данной сети для интерполяции. Если один вход (х) и один выход (у), то ошибка будет распространяться по всем нейронам скрытых слоев, и сеть будет как бы усреднять выходы. Например вход: 0, требуемый выход 0. Вход 2, требуемый выход 1000. При обучении первый случай будет уменьшать веса по всем связям, второй увеличивать.
Если выходов несколько, то проблема решается, а вот с одним не понятно.
Здравствуйте!
Скажите, если в сети есть нейрон смещения, то при обучении (обратное распространение ошибки) сети его вес тоже надо менять или он всегда постоянный?
Добрый день!
Для нейрона смещения, суть такая же, как и для "обычных" нейронов - ищем в процессе обучения "идеальный" вес связи, так что он тоже корректируется. При этом иногда может задаваться своя собственная скорость обучения именно для нейронов смещения, отличная от скорости для других нейронов.
δ7=(k∑δkwjk)⋅f′(I7)=(δ8⋅w78)⋅f′(I7) = 0.086⋅0.75⋅0.908⋅(1−0.908)=0.0054
δ6 = 0.086⋅0.75⋅0.54⋅(1−0.54)=0.016
Почему при расчёте ошибки на нейроне 7 делаете умножение 0.75 (выделил полужирным), хотя вес связи w78 = -0.22 (на картинке с перцептроном)? Ошибка вычисления или что-то не понял (тогда объясните)?
Опечатка, благодарю, поправлю.
А можно ли на вход подать нули (нет значений) и единицы (есть значения) на вход нейросети в задаче распознавания символов, где точки имеют цвет белый или черный, подойдёт ли 0 или 1? Ведь это ограничения сигмоидальной функции?
Сигмоида к значениям 0 и 1 стремится на бесконечности, поэтому можно пробовать и с нулями/единицами. Либо нормировать, к примеру - (0.001, 0.999).
Прошу прощения, в примере на этапе обратного прохода при вычислении дельта7 w78 = -0,22, а не 0,75 , так что как минимум одна ошибка в вычислениях присутствует.
Отлично, благодарю! В течение дня поправлю.
День добрый, Спасибо за статью.
Возможно опечатка, как получилось отрицательное число?
δ3=(−0.0016⋅0.34+0.016⋅2.2)⋅0.52⋅(1−0.52)=−0.0087
δ3=(−0,00054+2,216)⋅0.52⋅(1−0.52)=−0.0087
Да, похоже на то... спасибо, поправлю.
Всё здорово, кроме того, что смешение никак не корректируется !!!
Как не спросил...
В МОР веса корректируются. Смещения - нет. Это правильно?
А где там знак вопроса?
По существу - на практике можно встретить примеры как с коррекцией смещений, так и без. В целом, смещения должны корректироваться по такой же логике, при этом скорость обучения для них может быть иной (например, меньше, чем скорость обучения для "обычных" весовых коэффициентов).
не понятно от чего зависит Onet,k из за этого производную не получится взять, как в ней аргумент выглядит? мне интеграл брать теперь, чтобы понять как Onet выглядит
Производная везде от функции активации конкретного нейрона, Onet,k - это конкретное значение на выходе, соответственно берем производную и в нее подставляем это значение.
ладно, понял от чего зависят, единственное, кажись 2 потеряли при дифференцировании или мне так кажется
Да, похоже на то, спасибо.