Нейронная сеть Хопфилда. Обзор, обучение и пример работы.

Сегодняшняя статья будет посвящена еще одному типу сетей, а именно нейронной сети Хопфилда, которая представляет из себя автоассоциативную сеть, способную выполнять функцию памяти. Но не буду забегать вперед, обо всем по порядку.

Итак, сразу же поговорим об основных задачах, которые призвана решать сеть Хопфилда:

• Во-первых, конечно же, упомянутый вариант, когда сеть Хопфилда используется в качестве автоассоциативной памяти. Этому мы сегодня уделим наибольшее внимание.
• Во-вторых, для фильтрации данных.
• И, наконец, сеть также может быть применена для решения задач оптимизации.

Собственно, сразу же акцентируем внимание на первом из перечисленных пунктов. Суть заключается в том, что сеть может произвести восстановление ранее сохраненного образца по подаваемому на ее вход искаженному или неполному варианту.

Вероятно на данном этапе определение выглядит не совсем понятным, но сейчас на примере все встанет на свои места. Допустим мы хотим сохранить при помощи сети Хопфилда цифры от нуля до девяти (о процессе сохранения мы поговорим чуть позже, пока не будем останавливаться на этом моменте). Рассмотрим, например, цифру 2, представленную в следующем виде:

Пусть сеть уже обучена, то есть эту цифру, как и остальные, мы сохранили в памяти. Тогда, если мы подадим искаженный вариант сохраненной цифры на вход, сеть должна выдать нам правильное изображение (то, которое мы сохранили при обучении, без искажений). К примеру, подаваемый на вход образец может иметь следующий вид:

А в результате своей работы сеть должна выдать нам первый, неискаженный, вариант. В этом и состоит задача нейронной сети Хопфилда при использовании в качестве автоассоциативной памяти. Теперь обсудим структуру сети и непосредственно процесс обучения - запоминания образцов.

Структура нейронной сети Хопфилда.

Сеть Хопфилда является однослойной, в отличие от некоторых из рассмотренных нами ранее. Каждый из нейронов связан со всеми остальными, но не воздействует на себя самого.  В итоге получаем:

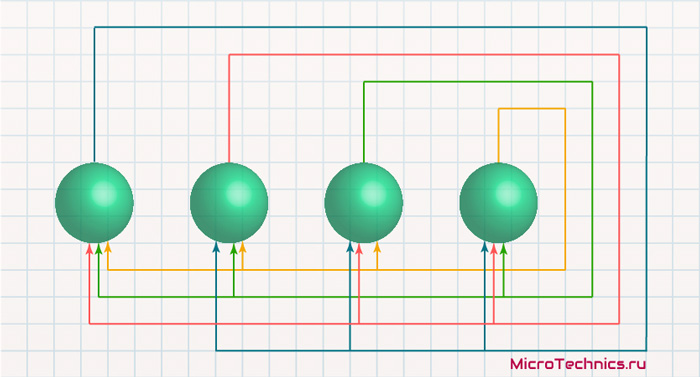
Соответственно, здесь мы имеем сеть из 4-х нейронов. В качестве функции активации нейронов сети Хопфилда используется пороговая функция:

s(x) = \begin{cases}
   \enspace 1 &\text {если } x > 0 \\
   -1 &\text {если } x < 0
\end{cases}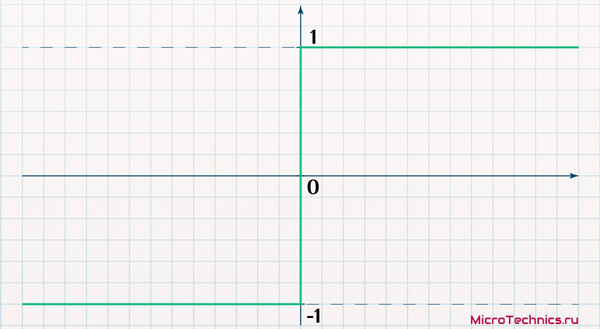

Комбинированный ввод, то есть сигнал на входе каждого из нейронов, вычисляется знакомым нам образом с использованием весовых коэффициентов связей:

x_j = \sum_{i=1}^{N}{s_i\medspace w_{ij}}

Здесь s_i - состояние нейрона с номером i. Если комбинированный ввод элемента оказывается отрицательным, то состояние элемента становится равным -1, напротив, когда комбинированный ввод положительный - состояние элемента соответствует +1. Если же x_j = 0, то нейрон не изменяет своего состояния, то есть сохраняет предыдущее.

Со структурой сети разобрались, переходим к процессу обучения.

Обучение нейронной сети Хопфилда.

Обучение сети Хопфилда значительно отличается от "привычных" алгоритмов обучения (например, от обучения по методу обратного распространения ошибки). В случае сети Хопфилда процедура обучения для одного входного образца (процедура сохранения образца) представляет из себя просто расчет весовых коэффициентов по вполне конкретной формуле:

W = x^Tx

Где W - это матрица весов, x - входной образец, а x^T - транспонированный вектор x (получается из исходного вектора заменой строк на столбцы). Если мы хотим сохранить несколько образцов (k штук), то необходимо произвести вычисления по этой формуле для каждого из образцов по отдельности, а затем сложить полученные матрицы W_k​:

W = W_1 + W_2 + ... + W_k

Таким образом, данный процесс, опять же в отличие от обучения сетей других типов, происходит всего лишь в один этап. Все перечисленные манипуляции для максимальной наглядности мы осуществим на практике в конце статьи, чтобы достигнуть полной гармонии с сетями Хопфилда 👍

Необходимо отметить еще один важный аспект. Как мы обсуждали в начале статьи, нейроны в сети Хопфилда не воздействуют сами на себя. Так вот, чтобы обеспечить выполнение этого условия, необходимо обнулить диагональные элементы в полученной в результате сохранения образцов матрице.

Итак, сеть обучена, осталось понять, как же она должна работать. В данном случае все довольно просто. Пусть мы подаем на вход искаженный элемент (например, все ту же цифру 2, почему нет). В результате работы сети состояния нейронов начинают меняться. И нам остается только ждать, пока сеть перейдет в устойчивое состояние - то есть в результате последующих обновлений ни один из нейронов не будет изменять своего состояния. В результате всех этих процессов мы получим сохраненный (неискаженный) вариант подаваемого на вход образца (вектора). Вот, собственно, и все.

Из этого вытекает следующий вопрос, к обсуждению которого и переходим.

Устойчивость сети.

Для успешной работы сети необходимо, чтобы нейроны перешли в некое устойчивое состояние, собственно, отсюда и вытекает вопрос – а будет ли сеть вообще устойчива? И здесь нельзя не рассмотреть два возможных режима работы:

1. Синхронный режим. Идея заключается в том, что расчеты для всех нейронов производятся последовательно, то есть по очереди. Но их состояния не меняются, а запоминаются. И лишь после того, как были пройдены все нейроны сети, их состояния одновременно изменяются на новые.
2. Асинхронный режим. Здесь отличие заключается в том, что состояния нейронов меняются не одновременно (не синхронно). То есть произвели расчеты для первого нейрона, в соответствии с чем установили его новое состояние. Далее производим вычисления для второго нейрона, но уже с учетом нового состояния первого. И также вслед за этим меняем состояние второго. И далее все по цепочке аналогично.

На практике в подавляющем числе случаев используется 2-й вариант, а именно асинхронный режим. И, возвращаясь к вопросу устойчивости, нейронная сеть Хопфилда, работающая в асинхронном режиме, всегда будет устойчива, что замечательно и безгранично радует.

Разберемся, из чего вытекает это свойство. Введем понятие функции энергии системы:

E = -\frac{1}{2}\medspace\sum_{j=1}^{N}{\sum_{i=1}^{N}{s_i\medspace s_j\medspace w_{ij}}}

При изменении состояния нейрона j на \Delta s_j​ энергия изменится на величину:

\Delta E = -\Delta s_j \sum_{i=1}^{N}{s_i\medspace w_{ij}}

Под знаком суммы у нас тут входной сигнал элемента элемента j. Таким образом, если сигнал на входе положительный, то и изменение состояния нейрона j положительное (\Delta s_j > 0). Аналогично, если \sum_{i=1}^{N}{s_i\medspace w_{ij}} < 0, то и \Delta s_j < 0. Поэтому изменение энергии всегда будет отрицательным (энергия будет уменьшаться в процессе работы сети), что и гарантирует нам то, что сеть является устойчивой.

Практический пример.

Итак, вернемся к той самой сети, которую мы рассмотрели в начале:

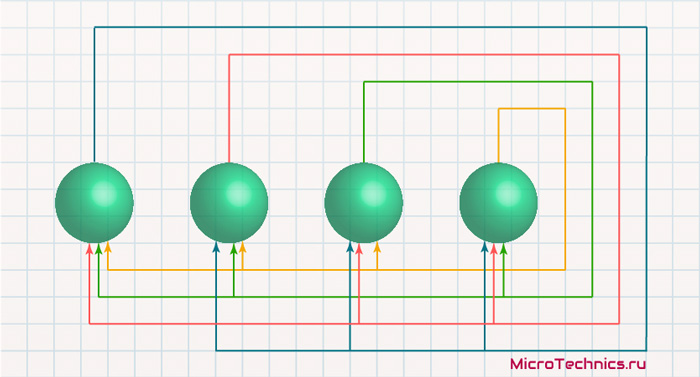
Запоминать будем образец x = [\medspace 1, \medspace 1, -1, -1\medspace ]. Определим весовую матрицу:

W = \begin{vmatrix} \hspace{0.6em} 1 \hspace{0.6em} \\ 1 \\ -1 \\  -1 \\ \end{vmatrix}\begin{vmatrix} \hspace{0.1em}1 & 1 & -1 & -1\hspace{0.1em} \end{vmatrix} = \begin{vmatrix} \hspace{0.6em} 1 & \hspace{0.6em} 1 & -1 & -1\hspace{0.6em} \\  \hspace{0.6em} 1 & \hspace{0.6em}1 & -1 & -1\hspace{0.6em} \\  \hspace{0.6em}-1 & -1 & \hspace{0.6em}1 & \hspace{0.6em}1\hspace{0.6em} \\  \hspace{0.6em}-1 & -1  & \hspace{0.6em}1 & \hspace{0.6em}1\hspace{0.6em} \end{vmatrix}

Обнуляем диагональные элементы:

W = \begin{vmatrix} \hspace{0.6em} 0 & \hspace{0.6em} 1 & -1 & -1 \hspace{0.6em} \\ \hspace{0.6em} 1 & \hspace{0.6em} 0 &  -1 & -1 \hspace{0.6em} \\  \hspace{0.6em} -1 & -1 & \hspace{0.6em}0 & \hspace{0.6em}1\hspace{0.6em} \\  \hspace{0.6em}-1 &  -1  & \hspace{0.6em} 1 & \hspace{0.6em}0 \hspace{0.6em} \end{vmatrix}

Прекрасно, сеть обучена и готова к работе. Подадим на вход искаженный образец, к примеру: x = [1, 1, -1, 1]. Последовательно осуществляем вычисления:

x_1 = 1 \cdot 0 + 1 \cdot 1 + (-1) \cdot (-1) + 1 \cdot (-1) = 1 \\
x_1 > 0 \rArr s_1 = 1 \\
x_2 = 1 \cdot 1 + 1 \cdot 0 + (-1) \cdot (-1) + 1 \cdot (-1) = 1 \\
s_2 = 1  \\
x_3= 1 \cdot (-1) + 1 \cdot (-1) + (-1) \cdot 0 + 1 \cdot 1 = -1 \\
s_3 = -1  \\
x_4 = 1 \cdot (-1) + 1 \cdot (-1) + (-1) \cdot 1 + 1 \cdot 0 = -1 \\
s_4 = -1 

В результате на выходе сети получили тот самый образец, который был ранее сохранен. Но на этом не все, необходимо убедиться, что сеть устойчива, а значит нейроны не изменят своего состояния при повторном проходе:

x_1 = 1 \cdot 0 + 1 \cdot 1 + (-1) \cdot (-1) + (-1) \cdot (-1) = 1 \\
s_1 = 1 \\
x_2 = 1 \cdot 1 + 1 \cdot 0 + (-1) \cdot (-1) + (-1) \cdot (-1) = 1 \\
s_2 = 1  \\
x_3= 1 \cdot (-1) + 1 \cdot (-1) + (-1) \cdot 0 + (-1) \cdot 1 = -1 \\
s_3 = -1  \\
x_4 = 1 \cdot (-1) + 1 \cdot (-1) + (-1) \cdot 1 + (-1) \cdot 0 = -1 \\
s_4 = -1 

Все четко по плану! Нейронная сеть Хопфилда выполнила свою функцию памяти и позволила нам восстановить сохраненный образец по подаваемому на вход искаженному варианту.

И на этой позитивной ноте завершаем сегодняшнюю статью, всем спасибо за внимание и до скорых встреч 🤝