Продолжаем обсуждение и изучение электронных компонентов под названием конденсаторы (ссылка). Основные аспекты устройства и принципа работы мы обсудили в предыдущей статье, а сегодня на очереди маркировка конденсаторов, а также разные варианты их соединения. Сначала разберем теорию, а затем рассмотрим несколько практических примеров. Собственно, приступим к делу.
Маркировка конденсаторов.
Существует несколько основных способов маркировки, давайте рассмотрим их в порядке очередности. Итак, один из вариантов - это маркировка тремя цифрами, например так:
В данном случае первые две цифры указывают на емкость конденсатора в пикофарадах (пФ), а третья обозначает множитель:
- если третья цифра от 0 до 5, то емкость в пикофарадах необходимо умножить на 10 в соответствующей степени. Степень как раз и определяется третьим числом
- если третья цифра - 8, то величину емкости умножаем на 0.01
- если третья цифра - 9, то величину емкости умножаем на 0.1
Давайте на практическом примере разберемся как же определить емкость, руководствуясь этими правилами - определим электроемкость изображенных на рисунке конденсаторов.
Для первого из них имеем маркировку "470" - первые две цифры - 47 - значит емкость равна 47 пФ. Множитель равен 0, тогда емкость определяется следующим образом:
C= 47 \cdot 10^0 = 47\medspace пФ
Запишем аналогичные выражения для последующих конденсаторов:
C_2= 15 \cdot 0.1 = 1.5\medspace пФ
C_3 = 22\cdot 10^3 = 22000\medspace пФ = 22\medspace нФ
C_4 = 47\cdot 10^4 = 470000\medspace пФ = 470\medspace нФ
C_5 = 68\cdot 10^2 = 680\medspace пФ = 6.8\medspace нФ
Как видите, здесь нет ничего сложного, поэтому плавно переходим к следующему способу.
Данный вариант маркировки почти не отличается от того, что мы уже обсудили. Отличие заключается только в том, что тут для обозначения величины емкости в пикофарадах используются три первые цифры (а не две), а четвертая цифра также обозначает множитель. Небольшой наглядный пример для этого случая и будем двигаться дальше:
По аналогии определяем емкость:
C = 475\cdot 10^2 = 47500\medspace пФ = 47.5\medspace нФ
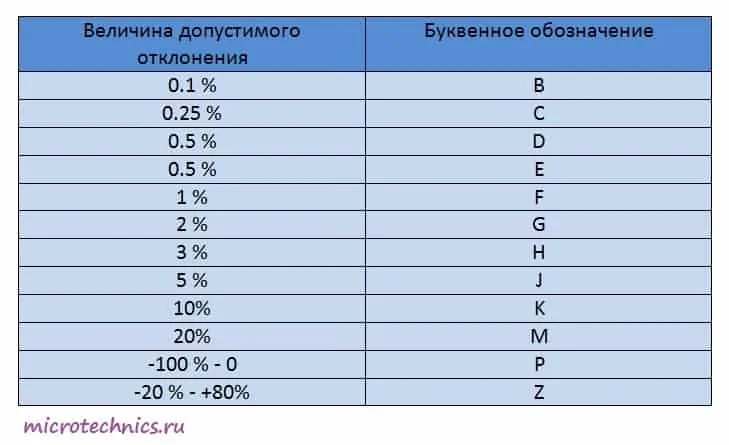
Иногда можно встретить маркировку тремя цифрами и буквой. В данном случае буква будет обозначать допустимое отклонение емкости от указанного цифрами значения:
Что именно означают эти цифры определяют в соответствии с таблицей:
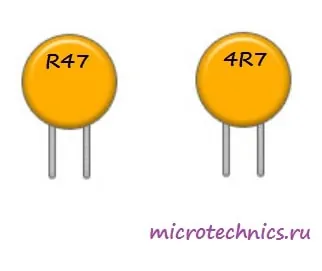
Кроме того, возможна цифровая маркировка непосредственно емкости в микрофарадах. Десятичная запятая в этом случае заменяется латинской буквой R:
Емкость здесь определяется очень просто (не забываем, что буква R просто заменяет запятую):
C_1 = 0.47\medspace мкФ
C_2 = 4.7\medspace мкФ
И, наконец, еще одним способом маркировки является цифро-буквенная маркировка. В данном случае величина емкости указывается цифрами, а единица измерения буквой:
- p - пФ
- n - нФ
- m - мФ
- u - мкФ
Причем здесь, также как и в предыдущем примере, если буква расположена между цифрами, то она выполняет роль десятичной запятой:
Определяем емкость:
C_1 = 1.5\medspace пФ
C_2 = 15\medspace нФ
C_3 = 33.5\medspace мкФ
C_4 = 1\medspace мФ
На этом мы заканчиваем обсуждение маркировки конденсаторов и переходим к вариантам их соединения.
Последовательное соединение конденсаторов.
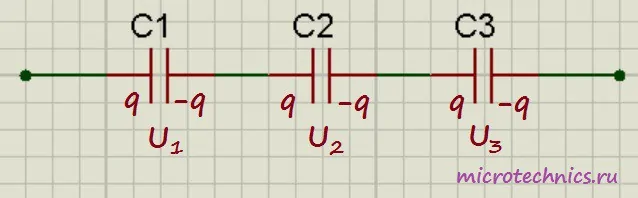
Как и в случае с резисторами первым делом рассмотрим последовательное соединение конденсаторов.
При таком соединении заряды всех конденсаторов окажутся равны:
q_1 = q_2 = q_3 = q
Вспомним формулу для напряжения из предыдущей статьи и определим величины:
U_1 = \frac{q}{C_1}U_2 = \frac{q}{C_2}U_3 = \frac{q}{C_3}А общее напряжение при последовательном соединении равно сумме напряжений на элементах схемы по отдельности:
U_0 = U_1 + U_2 + U_3
Но в то же время общее напряжение можно выразить через общую емкость цепи:
U_0 = \frac{q}{C_0}Приравниваем эти выражения и в результате получаем формулу для определения емкости при последовательном соединении конденсаторов:
\frac{1}{C_0} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3}Согласитесь, эта формула напоминает выражение для определения общего сопротивления при параллельном соединении резисторов (ссылка). С этим разобрались, продолжаем.
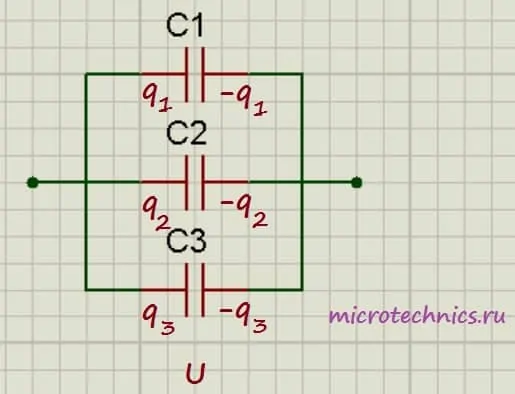
Параллельное соединение конденсаторов.
При параллельном соединении напряжения на конденсаторах равны:
U_1 = U_2 = U_3 = U
А заряды связаны следующим соотношением:
q_0 = q_1 + q_2 + q_3
Выразим напряжения на всех конденсаторах через их емкости и заряды:
q_1 = C_1\medspace U
q_2 = C_2\medspace U
q_3 = C_3\medspace U
Здесь мы учли, что напряжения равны. Данную систему можно условно заменить одним конденсатором, имеющим заряд q_0 и емкость C_0, напряжение на котором составляет величину U. Тогда будет справедливо следующее выражение:
C_0 = \frac{q_0}{U} = \frac{q_1 + q_2 + q_3}{U}\medspace=\medspace C_1 + C_2 + C_3Таким образом, при параллельном соединении конденсаторов их емкости складываются. Собственно, на этом наша сегодняшняя статья подходит к концу, надеюсь, что материал окажется полезным и понятным 👍















C2 = 15* 0.01 = 1.5 пФ
Мне кажется тут где то ошибка.
😀
Спасибо, 0 лишний напечатал.