И снова здравствуйте! 🙂 В продолжение моей предыдущей статьи хочу опубликовать и еще одну по смежной теме. А именно речь пойдет о структурной схеме, устройстве и принципе работы сигма-дельта модулятора. А на модуляторе уже базируются сигма-дельта аналого-цифровые преобразователи (АЦП). Постараюсь больше внимания уделить не стандартным общим словам, а конкретным примерам, чтобы лучше описать именно принцип работы.
Сигма-дельта модулятор.
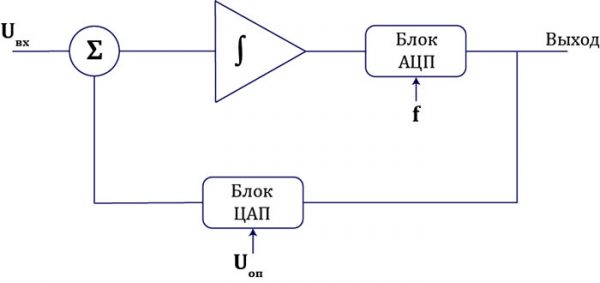
Структурная схема модулятора выглядит вот так:
Ключевые элементы схемы – сумматор (∑) и интегратор (∫). Кроме того, в схему входит блок АЦП, который преобразует аналоговое напряжение на выходе интегратора в биты. Эти биты идут как на выход, так и в цепь обратной связи. А в цепи обратной связи находится ЦАП, который на входе имеет эти же биты, а также определенное опорное напряжение. Итогом работы блока ЦАП будет аналоговое напряжение, которое поступает на сумматор. Пока это еще только теоретическая часть, из которой суть устройства далеко не очевидна, но обязательно рассмотрим и практический пример 🙂
Сигма-дельта АЦП.
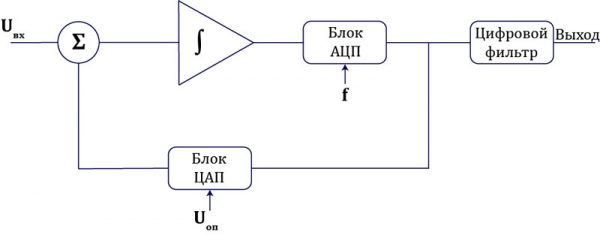
Дополнив модулятор блоком цифрового фильтра, получаем схему сигма-дельта АЦП:
И уже на выходе данного фильтра мы получим тот цифровой код, который нам и нужен. Если представить сигма-дельта АЦП в виде черного ящика, то на входе мы имеем аналоговое напряжение Uвх а на выходе цифровой код. При изменении Uвх меняется и этот код.
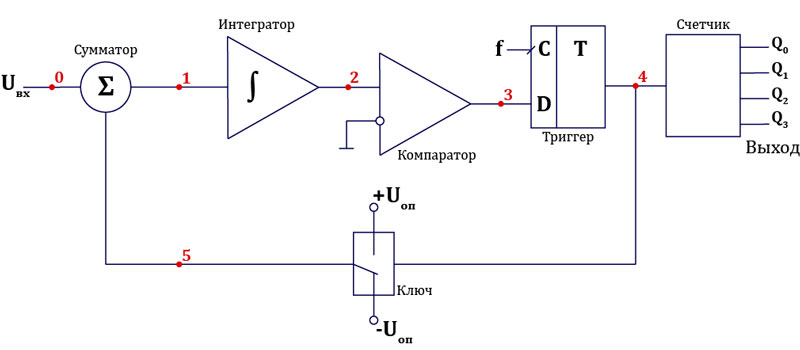
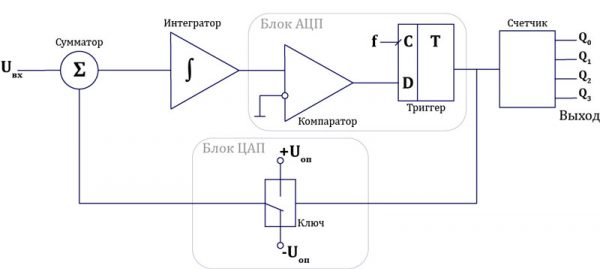
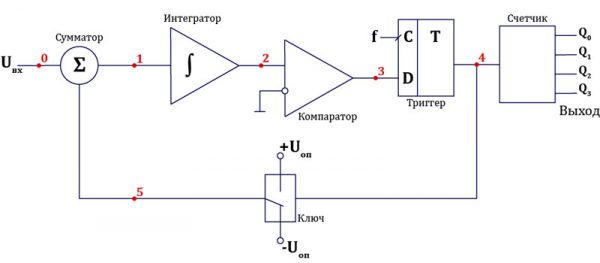
Теория теорией, но из нее принцип работы вынести не так просто. Поэтому попробуем разобрать небольшой пример реальной работы. И для этого рассмотрим АЦП первого порядка. Вообще такие АЦП бывают разных порядков – отличие в количестве сумматоров и интеграторов. Так преобразователь 5-го порядка содержит 5 сумматоров и 5 интеграторов. Но нас пока интересует первый порядок. Схема выглядит так:
Давайте соотнесем ее с общей схемой из начала статьи. Сумматор и интегратор остаются собой и на этой схеме, ключевые узлы, как ни крути. Блок АЦП первой схемы здесь состоит из компаратора и D-триггера с динамической синхронизацией. А блок ЦАП представляет из себя простой ключ. Работает он так:
| Вход, бит | Выход, В |
|---|---|
| 0 | Uоп |
| 1 | −Uоп |
В качестве же цифрового фильтра может быть использован 4-разрядный двоичный счетчик. Суть работы этого счетчика заключается в подсчете количества единиц на входе и выдаче на выходы цифрового кода, который соответствует этому количеству:
| Кол-во единиц |
Q3 | Q2 | Q1 | Q0 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
И далее аналогично до числа 15, поскольку счетчик 4-х разрядный. Для 4-х разрядов максимальный код на выходе равен 1111 (0x0F), что соответствует 15-ти. Получаем, что если на входе счетчика всегда нулевой уровень, то на выходах:
| Кол-во единиц | Q3 | Q2 | Q1 | Q0 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
Если на входе всегда «1», то на выходах:
| Кол-во единиц | Q3 | Q2 | Q1 | Q0 |
|---|---|---|---|---|
| 15 | 1 | 1 | 1 | 1 |
Аналогично для промежуточных значений на входе. И вот теперь самое интересное, подадим на вход АЦП напряжение и посмотрим, какие будут сигналы в разных частях схемы!
Принцип работы.
Пусть опорное напряжение равно 3В, а на входе сигма-дельта АЦП будет 2В: U0 = 2В, Uоп = 3В.
Схема будет менять свое состояние в соответствии с импульсами тактового сигнала на входе C триггера. Поэтому нам нужно разбить временную шкалу на части, которые равны периоду этого сигнала и определить, какие будут значения напряжений в разных точных схемы на разных интервалах.
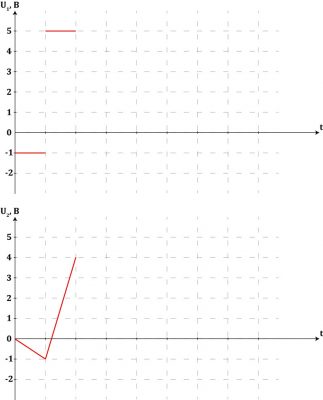
Интервал 1.
- Пусть в начальный момент времени в точке 4: 1. Это зависит от того, каким было состояние схемы на предыдущем шаге, поэтому можем принять любое значение в качестве начального.
- Значит на выходе ключа: U5 = −3В.
- Возвращаемся ко входу, на который по условию у нас поступило значение: U0 = 2В.
- В точке 1 будет: U1 = 2 − 3 = −1В.
В течении интервала 1 (также будет и для других интервалов) на входе интегратора постоянное напряжение. А значит на выходе интегратора будет «пила», наклон которой определяется величиной входного сигнала. В данном случае на входе U1 = −1В, значит напряжение на выходе интегратора изменится на −1В за этот промежуток времени:
- И в результате, имеем: U2 = −1В.
- Второй вход компаратора подключен к земле (0В), значит на его выходе будет 0, если U2 < 0. Так и происходит - точка 3: 0.
- По спаду импульса тактового сигнала эта величина попадает на выход триггера - точка 4: 0.
- И далее этот бит «0» идет на цифровой фильтр и в цепь обратной связи. Фильтр пока не трогаем, а вот ключ в данном случае изменит свое состояние, и мы получим: U5 = 3В.
Итак, мы разобрали в деталях работу всей схемы сигма-дельта модулятора на первом интервале.
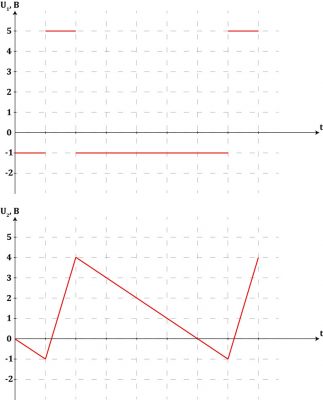
Интервал 2.
- На входе у нас все еще: U0 = 2В.
- Но на второй вход сумматора теперь поступает 3В, что дает на входе интегратора: U1 = 5В.
- С работой интегратора мы уже разобрались, так что определяем уровень на его выходе: U2 = 4В:
- Продолжаем, как и для интервала 1 - точка 3: 1, точка 4: 1, U5 = −3В.
Вот и второй интервал разобран. Составим таблицу и графики для этих и некоторого количества последующих отрезков:
| № | U0 | U1 | U2 | Точка 3 | Точка 4 (Выход) |
| 1 | 2В | −1В | −1В | 0 | 0 |
| 2 | 2В | 5В | 4В | 1 | 1 |
| 3 | 2В | −1В | 3В | 1 | 1 |
| 4 | 2В | −1В | 2В | 1 | 1 |
| 5 | 2В | −1В | 1В | 1 | 1 |
| 6 | 2В | −1В | 0В | 1 | 1 |
| 7 | 2В | −1В | −1В | 0 | 0 |
| 8 | 2В | 5В | 4В | 1 | 1 |
Здесь начиная с 7-го шага идет повторение всех процессов, поэтому мы легко можем продолжить ряд выходных значений. Для 15-ти интервалов получим:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
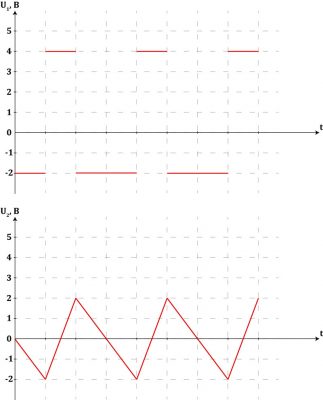
А если бы на вход приходил 1В, то результат был бы такой:
| № | U0 | U1 | U2 | Точка 3 | Точка 4 (Выход) |
|---|---|---|---|---|---|
| 1 | 1В | −2В | −2В | 0 | 0 |
| 2 | 1В | 4В | 2В | 1 | 1 |
| 3 | 1В | −2В | 0В | 1 | 1 |
| 4 | 1В | −2В | −2В | 0 | 0 |
| 5 | 1В | −4В | 2В | 1 | 1 |
| 6 | 1В | −2В | 0В | 1 | 1 |
| 7 | 1В | −2В | −2В | 0 | 0 |
| 8 | 1В | 4В | 2В | 1 | 1 |
В результате также имеем последовательность битов:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
Но это не совсем то, что нам требуется, поэтому в схеме присутствует еще и двоичный счетчик.
Счетчик подсчитывает количество единиц в подаваемой на его вход последовательности битов. При этом для 4-х разрядного счетчика максимальное количество подсчитанных единиц равно 15-ти. Потому что 15 единиц – это код 1111 (все четыре разряда = 1), после этого счетчик переполняется.
Давайте составим таблицу с полученными результатами для рассмотренных значений входного напряжения. При этом нас интересует период, равный 15-ти интервалам:
| Uвх | Кол-во единиц на входе счетчика | Q3 | Q2 | Q1 | Q0 |
|---|---|---|---|---|---|
| 2В | 12 | 1 | 1 | 0 | 0 |
| 1В | 10 | 1 | 0 | 1 | 0 |
Вот такой результат дает наша схема АЦП. Теперь можем проверить полученный на выходе цифровой код. Для 2В на входе на выходе счетчика мы получили код – 1100 (12 в десятичной системе счисления). При этом мы точно знаем, что при напряжении 3В на входе (равно опорному напряжению) на выходе модулятора у нас будут одни единицы. А на выходе счетчика мы получим «максимум», то есть код 1111 (15 единиц). А если на входе −3В, то на выходе модулятора сплошные нули, значит на выходе счетчика – 0000 (0). Опираясь на эти точки - (3, 15) и (−3, 0) - мы можем вывести формулу для расчета аналогового напряжения из цифрового кода:
U = (выход счетчика) / 15 * (3 + 3) − 3 = (выход счетчика) / 15 * 6 − 3
А теперь возьмем полученный нами код с выхода счетчика (1101) и рассчитаем для него аналоговое значение напряжения: U = 12 / 15 * 6 − 3 = 1.8В. Для второго полученного значения (1010): U = 10 / 15 * 6 − 3 = 1В
Здесь мы не попали точно в значение 2В из-за того, что накопили значения всего лишь для 15-ти интервалов. Поэтому шаг между соседними значениями напряжений достаточно велик. Например, для выходного кода 1101 (13), получаем значение U = 2.2В. То есть соседние значения равны 1.8В и 2.2В, и разность между ними значительна.
На этом моя статья подходит к концу, всем спасибо за прочтение, надеюсь было познавательно 🙂 Обязательно обратите внимание на дополнения к статье в комментариях ⬇️











Спасибо, что разъяснили суть работы. Правда, в конце сами запутались. На выходе должно быть ДВА счетчика. Один считает импульсы с выхода триггера, а второй циклический счетчик считает тактирующие импульсы f, идущие на вход C триггера. И при переходе второго счетчика из 11111 в 0000 (как вариант) значение первого счетчика подается на выход АЦП, а сам первый счетчик сбрасывается в 0000.
Спасибо за дополнение! Одна из первых моих статей, проба пера, поэтому отзыв особенно приятен )
Для фиксации показаний счётчика (того значения, которое получится после 16 (а не 15) интервалов тактовой частоты f, подаваемой на тактируемый D-триггер), её нужно подать на второй такоже счётчик до 15ти и передним фронтом сигнала его переполнения (переноса) синхронизировать запись состояния выходов первого счётчика в 4х-разрядный регистр, а задним фронтом - сбрасывать основной счётчик. Иначе он продолжит себе счёт дальше, и мы получим на выходе основного счётчика просто галопирующий циклический непрерывно инкрементируемый и обнуляемый двоичный код (число). В остальном - спасибо, единственное последовательное, и, потому, внятное описание принципа работы суммарно-разностного АЦП первого порядка. Было бы здорово для всех интересующихся продолжить тему и рассмотреть пример сигма-дельта АЦП более высокого порядка, чтобы расставить все точки над і.
Спасибо! В статью добавил рекомендацию изучить также и комментарии в обязательном порядке )
Как потом обратно преобразовать этот PDM сигнал в аналоговое напряжение?