Фильтр Калмана.

Как то так повелось, что очень нравятся мне всякие алгоритмы, имеющие четкое и логичное математическое обоснование ) Но зачастую их описание в интернете настолько перегружено формулами и расчетами, что общий смысл алгоритма понять просто невозможно. А ведь понимание сути и принципа работы устройства/механизма/алгоритма намного важнее, чем заучивание огромных формул. Как это ни банально, но запоминание даже сотни формул ничем не поможет, если не знать, как и где их применить 😉 Собственно, к чему все это.. Решил я замутить описание некоторых алгоритмов, с которыми мне приходилось сталкиваться на практике. Постараюсь не перегружать математическими выкладками, чтобы материал был понятным, а чтение легким.

И сегодня мы поговорим о фильтре Калмана, разберемся, что это такое, для чего и как он применяется.

Фильтр Калмана.

Начнем с небольшого примера. Пусть перед нами стоит задача определять координату летящего самолета. Причем, естественно, координата (обозначим ее $x_k$ ) должна определяться максимально точно.
Пример работы фильтра Калмана

На самолете мы заранее установили датчик, который и дает нам искомые данные о местоположении, но, как и все в этом мире, наш датчик неидеален. Поэтому вместо значения $x_k$ мы получаем:

$y_k = x_k + e_k$

где $e_k$ – ошибка датчика, то есть случайная величина. Таким образом, из неточных показаний измерительного оборудования мы должны получить значение координаты ( $x_{k,o}$ ), максимально близкое к реальному положению самолета.

Задача поставлена, перейдем к ее решению.

Пусть мы знаем управляющее воздействие ( $s_k$ ), благодаря которому летит самолет (пилот сообщил нам, какие рычаги он дергает 😉 ). Тогда, зная координату на k-ом шаге, мы можем получить значение $x_{k+1}$ на (k+1) шаге:

$x_{k+1} = x_k + s_k$

Казалось бы, вот оно, то что надо! И никакой фильтр Калмана тут не нужен. Но не все так просто.. В реальности мы не можем учесть все внешние факторы, влияющие на полет, поэтому формула принимает следующий вид:

$x_{k+1} = x_k + s_k + n_k$

где $n_k$ – ошибка, вызванная внешним воздействием, неидеальностью двигателя итп.

Итак, что же получается? На шаге (k+1) мы имеем, во-первых, неточное показание датчика $y_{k+1}$ , а во-вторых, неточно рассчитанное значение $x_{k+1}$ , полученное из значения $x_{k,o}$ на предыдущем шаге.

$x_{k+1} = x_{k,o} + s_k$

Идея фильтра Калмана заключается в том, чтобы из двух неточных значений (взяв их с разными весовыми коэффициентами) получить точную оценку искомой координаты (для нашего случая). В общем случае, измеряемая величина можем быть абсолютно любой (температура, скорость..). Вот, что получается:

$x_{k+1,o} = K_{k+1} * y_{k+1} + (1-K_{k+1}) * x_{k+1}$

Путем математических вычислений мы можем получить формулу для расчета коэффициента Калмана на каждом шаге, но, как условились в начале статьи, не будем углубляться в вычисления, тем более, что на практике установлено, что коэффициент Калмана с ростом k всегда стремится к определенному значению. Получаем первое упрощение нашей формулы:

$x_{k+1,o} = K * y_{k+1} + (1-K) * x_{k+1}$

где

$x_{k+1} = x_{k,o} + s_k$

А теперь предположим, что связи с пилотом нет, и мы не знаем управляющее воздействие $s_k$ . Казалось бы, в этом случае фильтр Калмана мы использовать не можем, но это не так 😉 Просто “выкидываем” из формулы то, что мы не знаем, тогда

$x_{k+1,o} = K * y_{k+1} + (1-K) * x_{k,o}$

Получаем максимально упрощенную формулу Калмана, которая тем не менее, несмотря на такие “жесткие” упрощения, прекрасно справляется со своей задачей. Если представить результаты графически, то получится примерно следующее:

Работа фильтра Калмана

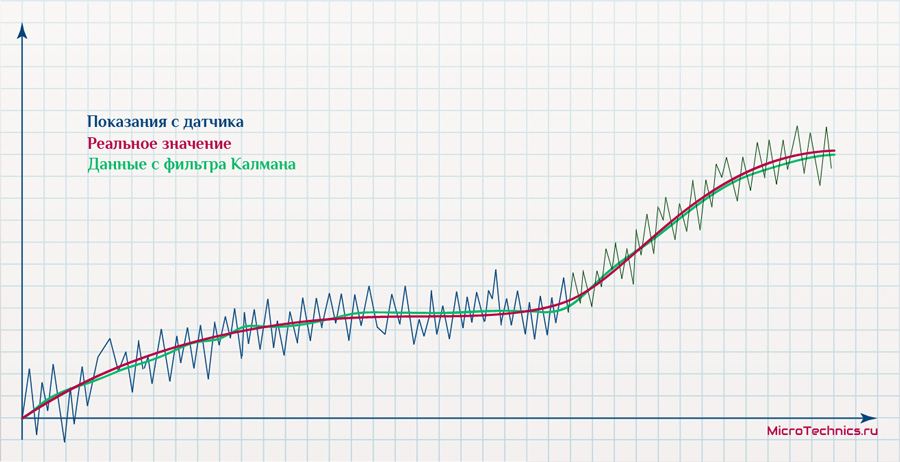
Если наш датчик очень точный, то естественно весовой коэффициент K должен быть близок к единице. Если же ситуация обратная, то есть датчик у нас не очень хороший, то K должен быть ближе к нулю.

На этом, пожалуй, все, вот так вот просто мы разобрались с алгоритмом фильтрации Калмана! Надеюсь, что статья оказалась полезной и понятной =)

Фильтр Калмана.: 6 комментариев

Nemo говорит 10.02.2014 в 17:34:

Лучше заменить красный или тёмно красный на другой цвет,так как сразу трудно разобрать где “показания датчика”, а где “реальное значение координаты”

Ответить ↓
- Aveal говорит 10.02.2014 в 19:30:
  
  Да, что-то я не подумал об этом..постараюсь переделать на днях)
  
  Ответить ↓
sim31 говорит 31.05.2014 в 17:09:

если к=0.5 получаем тупо среднее арифметическое
К(+1)=(К+Y)/2 помоему самый наглядный пример, половину данных взяли с датчика, половину от предыдущего значения.
Также этот фильтр работает как фильтр низких частот, можно обработать mp3 или wav файл и усилить басы хоть в 100500 раз, или задавить ВЧ помеху 🙂

Ответить ↓
кроссовер мен говорит 10.07.2014 в 16:53:

Классный фильтр для давки ВЧ. Если канеш у людей динамики взрослые, мона басы душить по полной )))

Ответить ↓
Старый_киповец говорит 24.09.2015 в 15:33:

Фильтр кальмана полезен если с измерениями туго, например акселерометр с чипом где период измерения 850 милисек ла ёщё и шифрование ноля. А где измерений прорва то пойдёт альфа-бета фильтр.

Ответить ↓
ls говорит 05.10.2016 в 13:55:

А можно ли подытожить для непонятливых?
X(k+1) = K * Y + (1-K)*X
То есть мы прогнозируем, что в настоящий момент измерения, координата Х равна некоему коэффициенту K умноженному на показание прибора + коэффициент (1-К) умноженному на значение Х на прошлом шаге.
При этом мы не уверены, что Х на прошлом шаге был верен? Не будет ли накапливаться ошибка?
Как собственно подобрать К? Может ли он корректироваться в процессе расчета, если мы понимаем, что можно делать вычисления точнее на следующем шаге?

Ответить ↓