Рассмотрев в подробностях структуру и принципы функционирования одного из классов нейронных сетей, а также обучение по методу обратного распространения ошибки, переходим к еще одному классу под названием – нейронные сети Кохонена. И далее логичным образом плавно перейдем к самоорганизующимся картам Кохонена.
Сходу можно выделить ключевое отличие от сетей, обучающихся по методу обратного распространения, которое заключается в том, что в случае с сетями Кохонена обучение протекает без учителя. Идея тут простая – как вы помните, обучающая выборка у нас состояла из наборов входных значений и соответствующих им выходных. При этом для обучения использовались все из этих данных, более того выходные значения не просто принимали участие в этой деятельности, а по сути играли ключевую роль. Это и есть обучение с учителем.
При обучении же без учителя используются только наборы входных данных, выходные вектора могут и вовсе отсутствовать, они просто не требуются. Как это осуществляется мы разберем как раз в этой статье, причем как в теории, так и на более чем конкретном реальном примере. В этом плане все по классике – лучшее понимание протекающих явлений дает именно совместное рассмотрение теоретических сведений и практическая демонстрация их работы.
Структура нейронной сети Кохонена.
Нейронная сеть Кохонена преимущественно используется для решения задач кластеризации, то есть объединения неких объектов в отдельные группы (кластеры). Решение о попадании объекта в тот или иной кластер принимается на основе значений его признаков, которые являются входными данными данного класса нейросетей.
Например, может стоять задача классификации спортсменов по виду спорта, которым они занимаются. Признаками могут быть рост, вес, время, за которое спортсмен пробегает стометровку и т. д. Если пропустить "параметры" всех спортсменов через сеть Кохонена, то на выходе мы получим определенное количество групп. При этом должны выполняться следующие условия:
- образцы, относящиеся к одной и той же группе должны быть подобны друг другу в некотором смысле
- а группы, подобные друг другу, в свою очередь, должны размещаться близко друг к другу
В данном примере все спортсмены, занимающиеся легко атлетикой, попадут в одну группу, а баскетболисты в другую. При дальнейшем обучении сети от группы легкоатлетов может отделиться группа бегунов. И тогда, следуя второму из перечисленных свойств, группа бегунов должна располагаться близко к группе легкоатлетов и далеко от группы баскетболистов. В дальнейшем, подавая данные признаков спортсмена на вход сети, мы получим результат, который заключается в определении, к какой группе (кластеру) данный спортсмен может быть отнесен.
Практический смысл заключается в том, что не всегда можно математическими или аналитическими методами сгруппировать имеющиеся объекты, нейронная же сеть Кохонена дает нам способ это осуществить. Причем механизм будет неизменен, какими бы не были имеющиеся данные.
Объектами могут являться, допустим, организации, а признаками - показатели прибыли, оборотный капитал, какие-либо еще данные из открытой финансовой отчетности. Нейронная сеть Кохонена может помочь в разделении этих фирм на группы более, либо менее благонадежных контрагентов, на основе чего уже можно принимать решение о целесообразности совместной деятельности с той или иной организацией.
Структурно сеть представляет из себя один входной слой и один выходной, причем все нейроны входного слоя связаны с каждым из нейронов выходного:
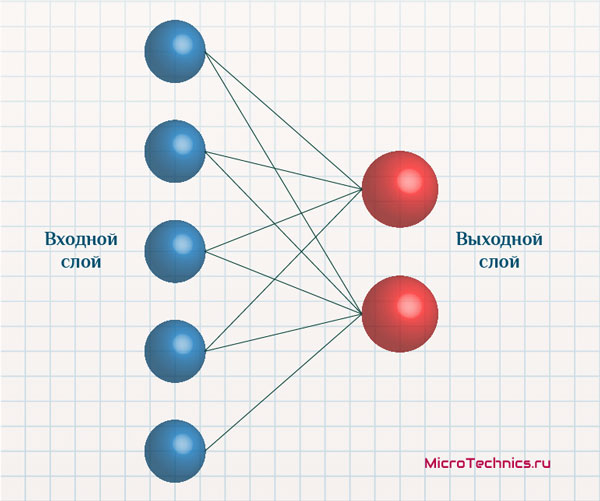
Число входных нейронов четко равно количеству признаков объектов, а количество выходных нейронов – числу кластеров. В работе сети действует принцип «победитель получает все», то есть наибольший выходной сигнал трансформируется в единичный, а остальные выходы обнуляются. Таким образом, подавая признаки некоторого объекта на вход, на выходе мы получим ряд нулевых значений, и лишь у одного нейрона значение будет равно единице. Это и сигнализирует о том, что объект отнесен к данному кластеру.
При этом удобно считать объекты, подаваемые на вход сети, векторами с координатами, равными значениям признаков:
x = \{x_1, \medspace x_2, \medspace x_3 \medspace ... \medspace x_n\}Аналогично выходные элементы также можно представить в виде векторов, координаты которых равны весам связей, приходящих к ним от нейронов входного слоя:
y_k = \{w_{1k}, \medspace w_{2k}, \medspace w_{3k} \medspace ... \medspace w_{nk}\}Здесь x - объект на входе, y_k - k-ый выходной нейрон, w_{1k} - весовой коэффициент связи между 1-м входным и k-ым выходным нейронами, аналогично и для остальных весов.
Обучение сети Кохонена аналогично другим типам сетей заключается в настройке весовых значений связей. Собственно, к данному аспекту и переходим.
Обучение нейронной сети Кохонена.
И тут я сразу разветвляю на две категории. Дело в том, что нейронная сеть Кохонена может обучаться, даже если изначальная структура сети неизвестна, каким бы странным это не казалось. Но начнем со случая, когда мы уже знаем количество признаков объектов исследования и число итоговых кластеров. Таким образом структура сети полностью определена и соответствует приведенной выше. Процесс обучения выглядит так, идем четко по шагам.
Этап 1.
Инициализируем весовые коэффициенты случайными значениями. Тут стоит остановиться на одном нюансе, в целом обычном для нейросетевых задач. И заключается он в том, что входные признаки обычно нормализуются так, чтобы их значения находились либо в диапазоне от -1 до 1, либо от 0 до 1.
В зависимости от этого вводятся ограничения на начальные веса связей:
- Нормализация выборки в пределах [-1; 1] – начальные значения весов должны удовлетворять соотношению |w_{ij}| \le \frac{1}{\sqrt{n}}, где n – это число признаков, оно же – число нейронов входного слоя.
- Нормализация выборки в пределах [0; 1] – и для этого случая: 0.5 - \frac{1}{\sqrt{n}} \le |w_{ij}| \le 0.5 + \frac{1}{\sqrt{n}} .
Этап 2.
На входы сети подаются значения из обучающей выборки, то есть признаки одного из исследуемых объектов. И для этих значений производится расчет евклидовых расстояний от входного вектора до центров каждого из кластеров в отдельности (пусть всего K кластеров - выходных нейронов):
R_j = \sqrt{\sum_{i}^n{(x_i - \medspace w_{ij})^2}}В данном соотношении участвуют:
- R_j - евклидово расстояние от текущего вектора на входе до j-го выходного нейрона.
- n - число признаков, оно же - число входных нейронов.
- x_i - значение i-го признака текущего объекта на входе.
- w_{ij} - вес связи между i-м входным нейроном и j-м выходным.
Этап 3.
Полученные на втором этапе значения R_1, \medspace R_2, \medspace R_3 \medspace ... \medspace R_K анализируются на предмет поиска минимального из них. Пусть минимальным оказался R_k, тогда выходной нейрон k объявляется победитилем и начинается корректировка весовых коэффициентов в соответствии с соотношением:
w_{ik \medspace new} = w_{ik \medspace old} + \eta(s) \medspace (x_i - w_{ik \medspace old})Снова разбираем действующих лиц:
- w_{ik \medspace old} - текущее значение весового коэффициента.
- w_{ik \medspace new} - новое значение.
- x_i - значение i-го признака текущего объекта на входе.
- \eta(s) - скорость обучения.
Отдельно необходимо остановиться на функции \eta(s), которая представляет из себя скорость обучения нейронной сети. При этом ее задают убывающей с течением времени, в данном случае s - текущая итерация обучения. Таким образом весовые коэффициенты нейрона-победителя будут изменяться все в меньшей степени по мере протекания процесса, например:
\eta(s) = \frac{\eta_0}{s}{\eta_0} - некое начальное значение для первой итерации обучения, когда s = 1.
Этап 4.
Данные шаги (начиная со 2-го) повторяются пока не выполнится условие окончания обучения. В качестве такого условия могут быть разные варианты. Например, таким фактором может выступать время, затраченное на обучение. То есть по прошествии этого фиксированного времени процесс обучения прерывается и завершается. Также может быть задано количество эпох обучения, и опять же по достижению данной величины процесс финиширует.
Переходим ко второму случаю, когда изначально структура сети является неизвестным параметром. То есть выходные нейроны отсутствуют, тогда действуем в соответствии со следующим механизмом.
Отправной точкой является некое значение евклидова расстояния R_0, которое соответствует максимально допустимому расстоянию от нейрона-победителя до входного вектора.
На вход сети аналогичным образом подается один из элементов, то есть признаки-координаты входного вектора из обучающей выборки. Также как и в описанном выше случае, происходит расчет евклидовых расстояний от этого вектора до каждого из существующих выходных нейронов:
R_j = \sqrt{\sum_{i}^n{(x_i - \medspace w_{ij})^2}}Находится минимальное из полученных значений и определяется выходной нейрон-победитель. Пусть это значение R_{k1} и, соответственно, нейрон-победитель k1.
Если выполняется соотношение R_{k1} \le R_0 то происходит корректировка весов связей нейрона-победителя (k1) все по той же формуле:
w_{ik \medspace new} = w_{ik \medspace old} + \eta(s) \medspace (x_i - w_{ik \medspace old})Отличие наблюдается для противоположного случая, то есть когда R_{k1} > R_0. В данном случае в нейронную сеть добавляется новый выходной нейрон. И его весовые коэффициенты задаются равными текущему входному вектору, который мы подали на вход сети.
Из этого логично вытекает, что на первой итерации обучения в любом случае будет добавлен выходной нейрон, просто потому что изначально их попросту нет, и евклидово расстояния высчитывать не из чего.
Ну и далее процесс циклически повторяется. Все это мы визуализируем на наглядном примере, а пока перейдем к следующему подразделу.
Самоорганизующиеся карты Кохонена.
Самоорганизующаяся карта Кохонена (SOM - Self-Organizing Map) – это одна из версий нейронных сетей Кохонена, поэтому все, что мы обсудили, остается в силе. Ключевой момент заключается в том, что использование карт Кохонена позволяет отобразить результаты своей работы в виде удобных для понимания карт (чаще всего двумерных). И уже на основе наглядной графической интерпретации можно с комфортом производить анализ полученных данных, поиск зависимостей, прогнозирование и т. д.
Таким образом, карты Кохонена позволяют преобразовать исходное n-мерное пространство в пространство меньшей размерности, с которым уже гораздо проще взаимодействовать.
Выходные нейроны самоорганизующейся карты чаще всего изображают расположенными в виде двумерной сетки:
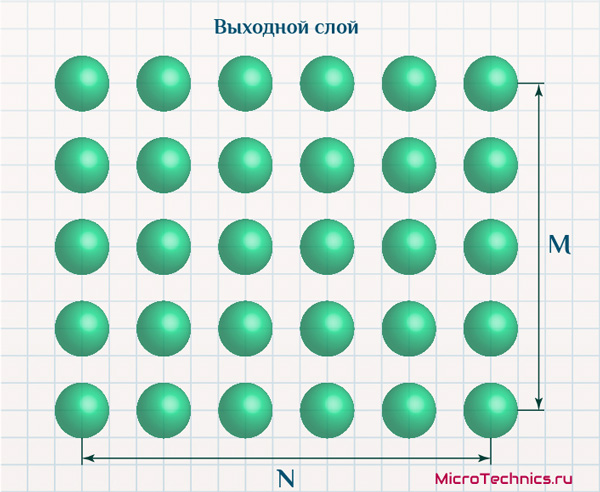
Но при этом каждый из них по-прежнему характеризуется, в первую очередь, значениями своих весовых коэффициентов:
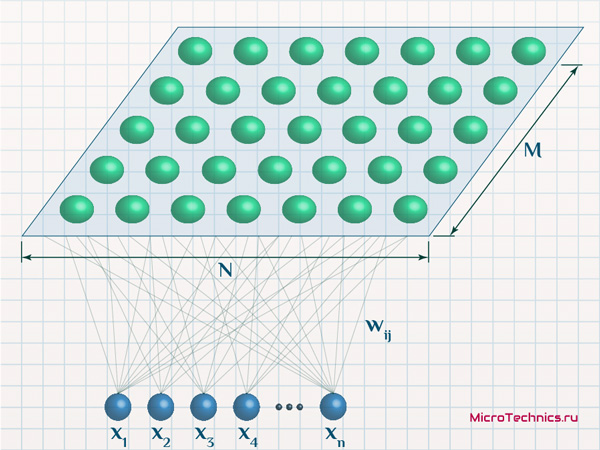
То есть суть и логика остаются такими же как мы обсудили, просто добавляется нюанс в виде упорядоченного размещения выходных нейронов, которое позволяет наглядно увидеть результаты работы сети. Очевидно, что n-мерное пространство, элементами которого, по сути, и являются нейроны выходного слоя, их координаты - y_k = \{ w_{1k}, \medspace w_{2k}, \medspace w_{3k} \medspace … \medspace w_{nk} \}, отобразить на экране или бумаге невозможно. Иначе дело обстоит в данном случае, когда нейроны условно располагают в виде 2D-сетки, которая легко может быть представлена графически. По существу - это очень изящное решение и красивая идея 👍
Процесс обучения протекает в сущности так же, как и для общего случая нейронных сетей Кохонена, то есть по тем шагам, которые мы уже детально обсудили, но есть одно важное отличие.
Заключается оно в том, что обновление значений весов осуществляется не только для нейрона-победителя, но также и для некоторых соседних нейронов. Каких именно соседей - определяется функцией соседства h_{kj}(t), которая определяет «меру соседства» выходных нейронов. Чаще всего применяется вариант, когда данная функция представляет гауссовскую функцию:
h_{kj}(s) = e^{\frac{-d_{kj}^2}{2\sigma^2(s)}}- k - номер нейрона-победителя.
- j - другой выходной нейрон.
- s - текущая итерация процесса обучения.
- \sigma(s) - обучающий сомножитель, значение которого убывает с увеличением s.
- d_{kj} - евклидово расстояние между нейронами k и j.
Функция убывает как с течением времени, так и с увеличением d_{kj}. А обновление весовых коэффициентов происходит по формуле:
w_{ij \medspace new} = w_{ij \medspace old} + \eta(s) \medspace h_{kj}(s) \medspace (x_i - w_{ij \medspace old})Замечаем, что обновляется не только вес w_{ik} для k-го нейрона-победителя, но и веса для других выходных нейронов w_{ij}. Кроме того, добавляется упомянутая функция соседства, которая и определяет, в какой мере будет скорректирован вес того или иного нейрона. Если нейрон j сильно удален от нейрона-победителя k, то значение h_{kj}(s), в свою очередь, тоже будет мало.
Давайте вычислим, что произойдет непосредственно для нейрона-победителя, то есть примем j равным k. Функция соседства превращается в:
h_{kk}(s) = e^{\frac{-d_{kk}^2}{2\sigma^2(s)}} = e^{\frac{0}{2\sigma^2(s)}} = 1Очевидно, что d_{kk} - расстояние от k-го нейрона до него же самого - равно 0. Тогда:
w_{ik \medspace new} = w_{ik \medspace old} + \eta(s) \medspace h_{kk}(s) \medspace (x_i - w_{ik \medspace old}) = w_{ik \medspace old} + \eta(s) \medspace (x_i - w_{ik \medspace old}) И получаем в точности ту первую формулу, которую мы рассматривали, что абсолютно логично. Резюмируем, таким образом, что отличие процесса обучения кроется именно в том, что обновляются значения не только для нейрона-победителя, но и для его соседей. Механизм же по сути неизменен.
Итак, продолжаем... Подаем на вход данные одного из объектов, определяем нейрон-победитель, а затем для него и его соседей производим обновление весовых коэффициентов:
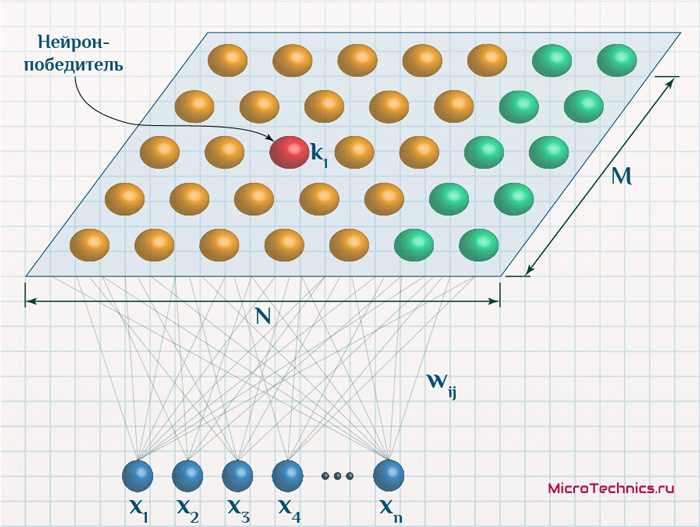
В соответствии с функцией соседства, по мере протекания процесса обучения, все меньшее число соседей будут подвергаться обновлению (для "далеких" соседей значений функции соседства будет мало, для простоты пренебрежем им):
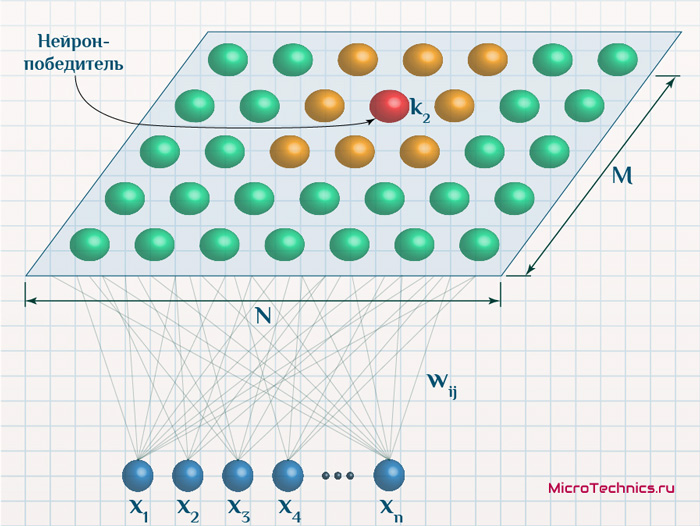
Зачастую применяется терминология, что при корректировке весов нейрон-победитель и его соседи перемещаются ближе к тому объекту, который был подан на вход на данной итерации. И это действительно отлично описывает процесс, только формулировка не дает четкого понимания, что именно имеется ввиду. Скорее даже вводит в заблуждение, если в нее не вникнуть. Мы же разберем более подробно, чтобы исключить любые неочевидные и вызывающие вопросы моменты.
Итак, рассмотрим вариант самоорганизующейся карты Кохонена, и подадим на вход один из объектов:
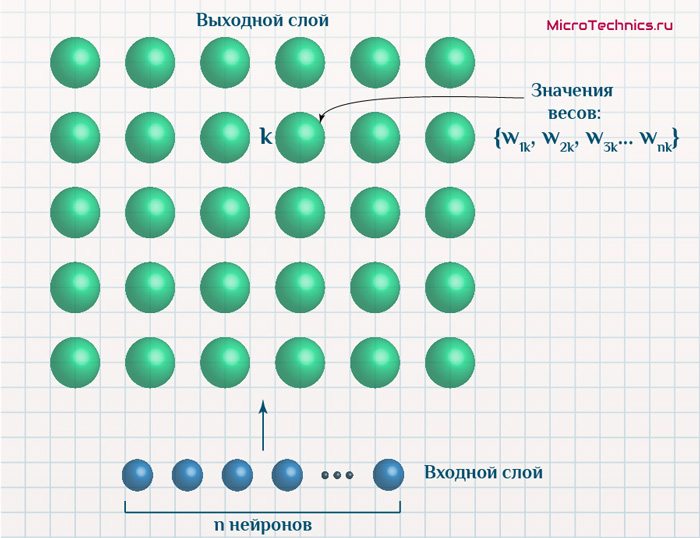
И ключ заключается в том, что на самом деле у нас имеется два пространства – n-мерное пространство, в котором координаты нейрона k равны \{ w_{1k}, \medspace w_{2k}, \medspace w_{3k} \medspace … \medspace w_{nk} \}. Кроме того, двумерное пространство, в рамках которого мы графически разместили выходные нейроны. Пусть значения признаков подаваемого объекта таковы x_0 = \{ x_{01}, \medspace x_{02}, \medspace x_{03} \medspace … \medspace x_{0n} \}.
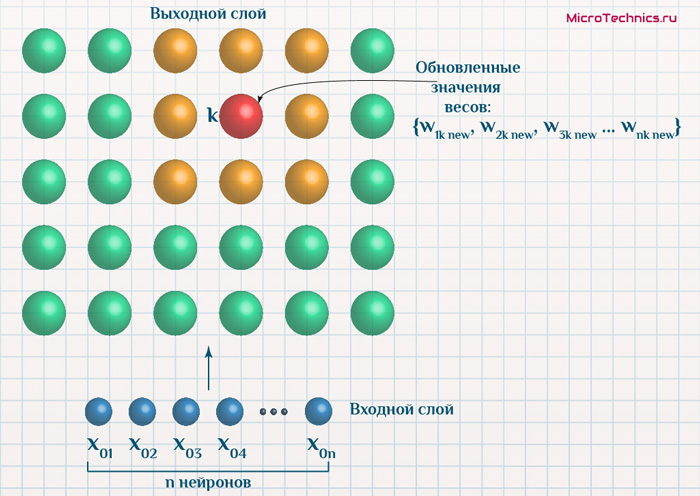
Допустим, нейроном-победителем оказался нейрон k, а его соседями, которые на данном этапе будут подвергаться обновлению – нейроны, обозначенные желтым.
Координаты нейрона k до обучения:
y_k = \{w_{1k}, \medspace w_{2k}, \medspace w_{3k} \medspace ... \medspace w_{nk}\}После же итерации обучения:
y_{k \medspace new} = \{w_{1k \medspace new}, w_{2k \medspace new}, \medspace w_{3k \medspace new} \medspace ... \medspace w_{nk \medspace new}\}И итогом является то, что он действительно становится ближе к объекту x_0 с координатами (значениями признаков) \{ x_{01}, \medspace x_{02}, \medspace x_{03} \medspace … \medspace x_{0n} \}. Вот только подразумевается здесь близость именно в контексте имеющегося n-мерного пространства. То есть вектор y_{k \medspace new} = \{ w_{1k \medspace new}, \medspace w_{2k \medspace new}, \medspace w_{3k \medspace new} \medspace … \medspace w_{nk \medspace new} \} ближе к вектору x_0 = \{ x_{01}, \medspace x_{02}, \medspace x_{03} \medspace … \medspace x_{0n} \}, чем изначальный y_k = \{ w_{1k}, \medspace w_{2k}, \medspace w_{3k} \medspace … \medspace w_{nk} \}. В двумерном же виде выходные нейроны остаются расположены ровно также.
На практике я часто сталкивался с путаницей именно касаемо этого вопроса, поэтому и было решено углубиться подробнее в эту ситуацию. А тем временем двигаемся дальше. И во имя наибольшего погружения в саму суть темы, конечно, рассмотрим ряд наглядных примеров.
Самоорганизущиеся карты Кохонена. Примеры.
Пример 1.
Допустим, у нас есть набор из 100000 объектов, каждый из которых имеет свой цвет. RGB-составляющие цвета – это три значения, соответственно объекты имеют по 3 признака. Выходных нейронов пусть будет 400, их разместим в виде сетки размером 20 на 20 (графически представим каждый из них в виде прямоугольной ячейки).
Значения весовых коэффициентов инициализируем случайными величинами, а для визуализации каждый из нейронов изобразим в цвете, причем этот цвет будет соответствовать его весовым коэффициентам. Так для нейрона с весами {255, 0, 0} цвет будет красным. На старте имеем следующее:
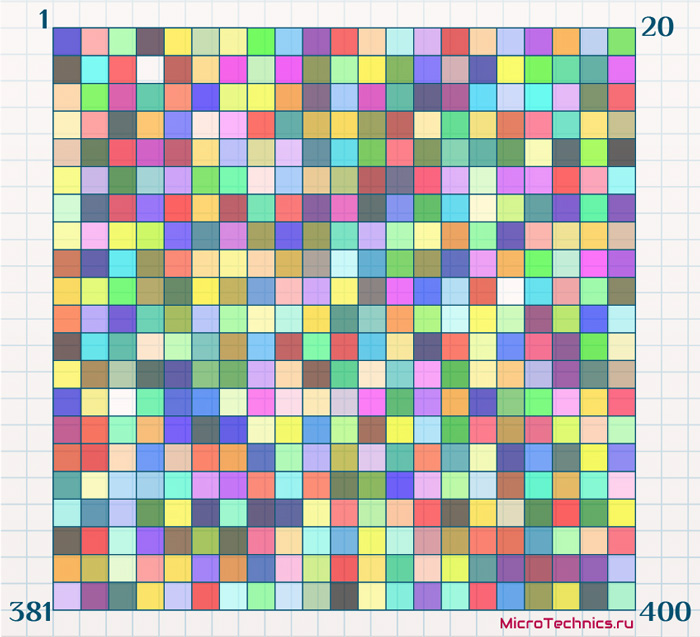
Поскольку весовые коэффициенты проинициализированы случайными величинами, то и цвета нейронов аналогично случайны.
В качестве обучающей выборки используем упомянутые 100000 объектов, только не каких-то конкретных, а случайно сгенерированных, что позволит их признакам быть распределенными более-менее равномерно. Проводим обучение самоорганизующейся карты Кохонена путем поочередной подачи каждого из объектов обучающей выборки на вход сети. И в результате получаем:
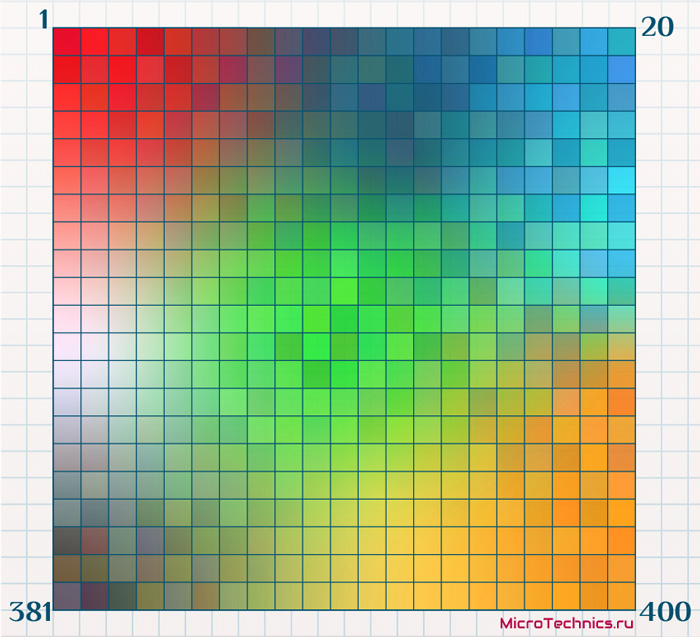
Что соответствует рассмотренной нами логике обучения.
При подаче на вход одного из элементов происходит корректировка нейрона-победителя и соседей, влекущая за собой «перемещение» этих нейронов «ближе» к входному вектору. Что в данном случае означает изменение цвета. То есть, если на входе у нас объект с признаками {0, 255, 0} (цвет – зеленый), то нейрон-победитель и его соседи изменят свои веса так, что их значения станут «ближе» к {0, 255, 0} (а это значит, что их цвета станут «более зелеными»).
При разборе нейронных сетей Кохонена в начале статьи мы использовали термин «кластер», причем каждый выходной нейрон соответствовал одному кластеру. В случае с самоорганизующимися картами Кохонена смысл кластера становится чуть другим. Кластером будет являться группа нейронов выходного слоя, расстояние между которыми меньше, чем расстояние до соседних групп. Таким образом для нашего примера может быть следующая картина:
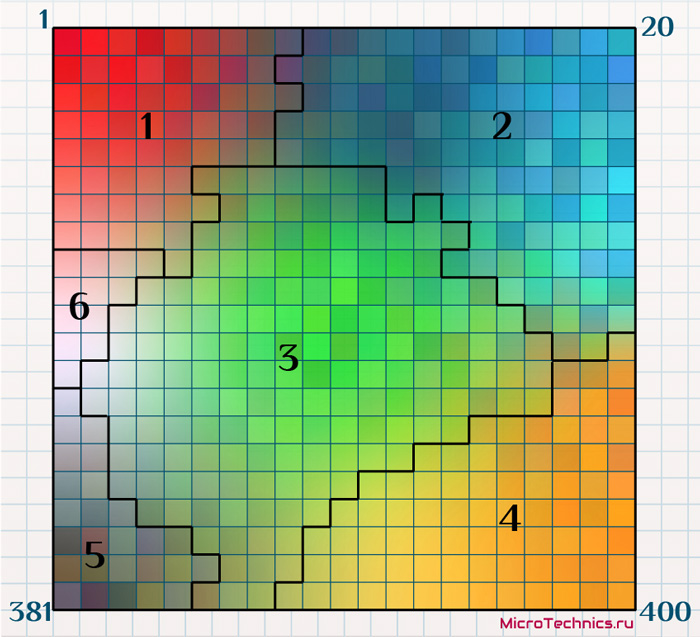
Как видите, группы нейронов, имеющих схожие значения признаков (а значит и цвет при таком графическом отображении) сгруппированы в кластеры.
Пример 2.
В предыдущем примере мы ввели окраску нейронов в соответствии со всеми тремя его признаками. Обычно же бывает несколько иначе. Пусть на этот раз в качестве объектов для исследования выступают некоторые организации, вкратце мы такой вариант уже обсуждали в начале статьи. Признаками будут какие-либо данные финансовой отчетности – доходы, оборот, количество сотрудников и что-либо еще аналогичное. Всего, допустим, признаков 10, а объектов, которые будут использованы для обучения – 10000. Сформируем самоорганизующуюся карту Кохонена с выходными нейронами в виде сетки 20 на 20.
Обучаем сеть, получаем измененные значения весовых коэффициентов, при этом нейроны структурированы все также.
А теперь, окрашивая полученную карту в соответствии со значением какого-либо из 10-ти признаков, мы получим наглядное представление результатов. К примеру, первый признак – это доход компании за предыдущий отчетный период. Среди 10000 объектов, которыми мы оперировали при обучении, минимальное значение – 0.1 млрд, максимальное – 1 млрд. Примем, что 0 млрд – это черный цвет, а 1 млрд – красный, и окрасим выходные нейроны в соответствии со значением первого признака каждого из них. Так выходной нейрон с координатами-признаками \{ 1, \medspace x_2, \medspace x_3 \medspace ... \medspace x_n \} будет окрашен в красный цвет \{ 255, \medspace 0, \medspace 0 \}, а с координатами \{ 0.5, \medspace x_2, \medspace x_3 \medspace ... \medspace x_n \} – в промежуточный между черным и красным \{ 127, \medspace 0, \medspace 0 \} (0.5 здесь - это доход 0.5 млрд).
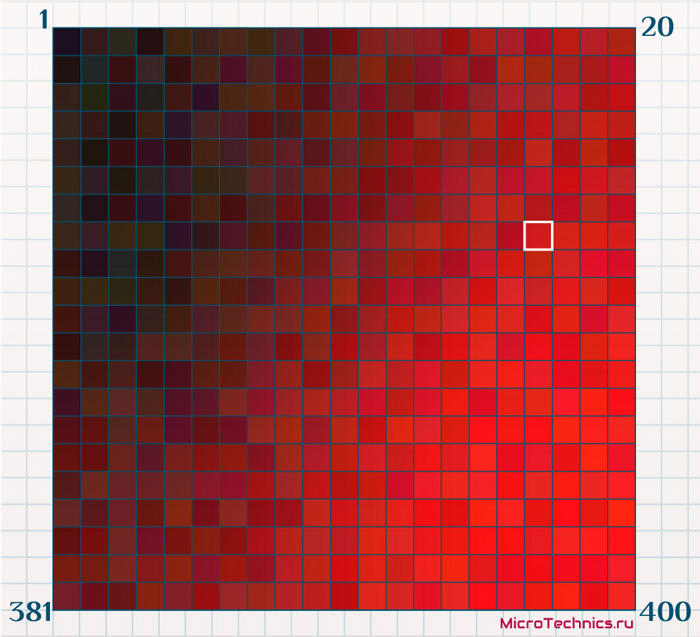
Итого, мы, во-первых, исходный набор из 10000 объектов с 10-ю признаками каждый сузили до наглядного представления в виде сетки из 400 ячеек. И, во-вторых, можем анализировать данные путем такой вот окраски ячеек в зависимости от значения того или иного признака. Здесь мы имеем карту, по которой можем оценить доходы организаций.
Построим еще одну, в которой окраска будет производиться в зависимости от того, сколько объектов из выборки попали в ту или иную ячейку. Поскольку исходных объектов больше, притом на порядок, чем ячеек-нейронов, то логично, что в большинство из ячеек попали несколько объектов. Пусть максимальное число объектов в одной из ячеек равно 45, а минимальное - 4. Зададим для 45 – синий цвет, для 4 – белый:
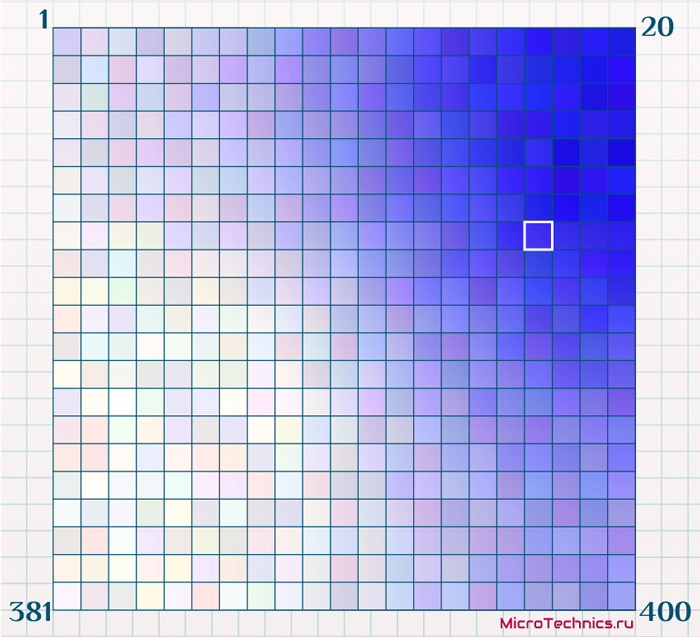
Имеем наглядную демонстрацию, как распределены объекты по ячейкам карты Кохонена. И это дает нам отличный механизм для анализа данных, в данном конкретном примере, на основе всего двух окрашенных вариантов мы уже можем сделать определенные выводы:
- Большинство организаций имеют средний доход. Из второй карты видим, что подавляющее число объектов расположены в правом верхнем углу. А по первой карте делаем вывод, что доход в этой области средний (цвет навскидку плюс-минус между красным и черным).
- Рассмотрим выделенную белым ячейку. По первой карте можем сделать вывод о среднем доходе, по второй - о количестве организаций, попавших в эту группу. Далее эту информацию можно использовать для какого-либо последующего финансового анализа.
- Из первой карты наглядно видны две области: минимальный доход - верхний левый угол, максимальный - нижний правый. Из второй же можно сделать вывод, что преуспевающих фирм больше, чем неуспешных (более синий цвет нижнего правого угла относительно верхнего левого).
Более того, на основе полученных данных можно произвести и прогнозирование. Например, помимо набора из 10-ти признаков, которые участвовали в обучении, существует еще один фактор - перспективность вложений в акции фирмы. Для имеющихся 10000 объектов данный фактор известен (но не принимал участия в обучении), но есть ряд организаций, для которых фактор не определен. Для каждой ячейки найдем среднее значение «перспективности» (взяв значения отнесенных к ячейке объектов и усреднив). Далее обученную карту Кохонена окрасим в соответствии с новый фактором, более перспективные ячейки – золотой, менее – черный:
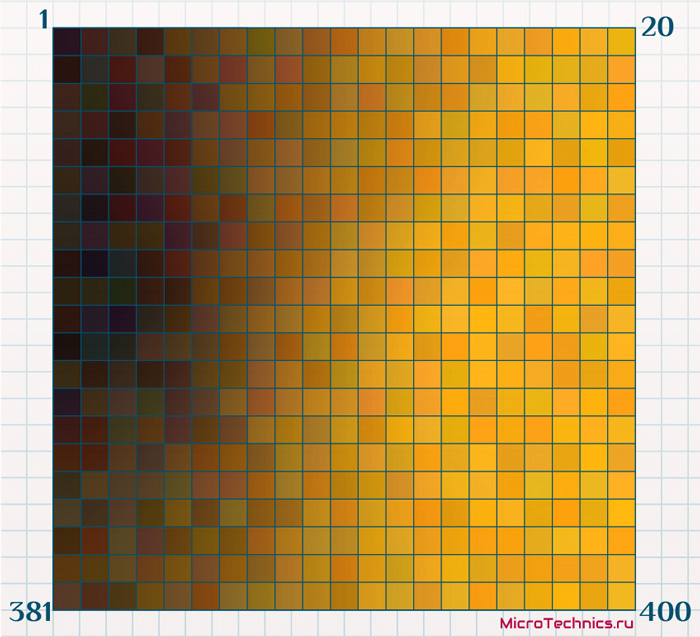
А теперь берем новую организацию, для которой из финансовой отчетности взяты 10 признаков, но «перспективность» не известна, и подаем ее на вход сети. В результате этот новый объект будет отнесен к какой-либо из ячеек:
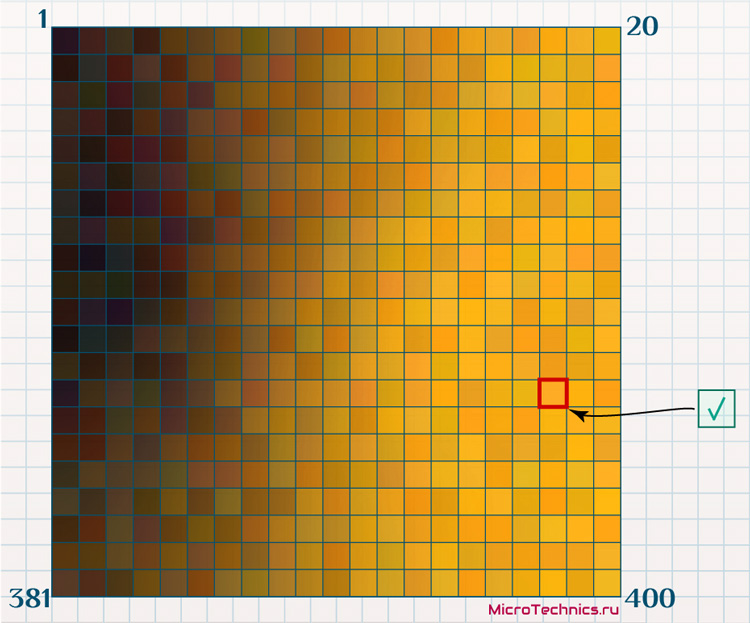
Новая точка располагается довольно близко к наиболее «перспективным» (золотым) ячейкам, что сигнализирует о том, что вполне резонным может оказаться прогноз о том, что и в эту организацию имеет смысл инвестировать.
Так что польза от использования нейронных сетей Кохонена неоспорима.
Пример 3.
Пробежимся еще по двум примерам, поскольку не могу оставить их в стороне. Эти примеры являются наверно самыми популярными при обзоре самоорганизующихся карт Кохонена, но фактически нигде не описаны явно некоторые моменты, которые на мой вкус и по моим наблюдениям являются не всегда очевидными.
Итак, первая задача. Имеется 500 объектов, каждый из которых имеет по два признака. Причем объекты таковы, что если на двумерной плоскости по оси x отложить значение первого признака, а по оси y – второго, получим такое размещение:
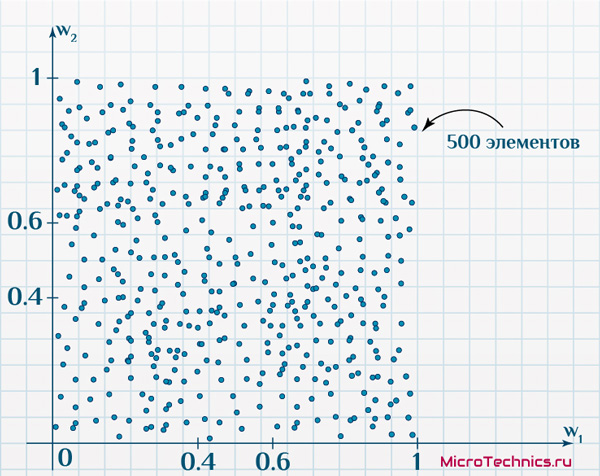
По осям – значения признаков исследуемых объектов (диапазон для обоих признаков: от 0 до 1). Карта Кохонена будет иметь на выходе сетку из 100 нейронов (10 на 10).
Веса связей снова проинициализируем случайными величинами, пусть из интервала (0.4, 0.6), и отобразим выходные нейроны на той же плоскости со значениями признаков по осям:
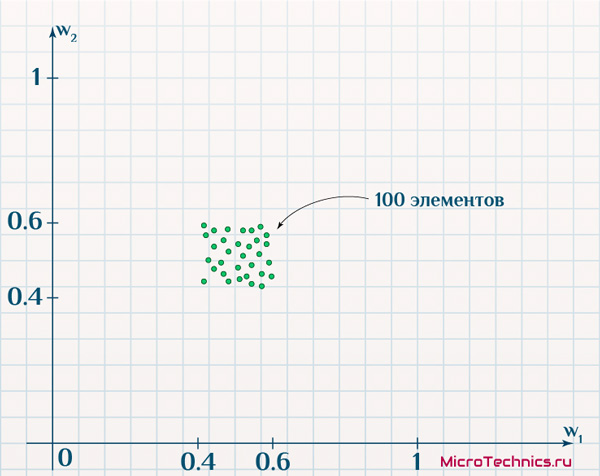
И вот тут часто возникает путаница, поскольку на выходе у нас двумерная сетка, и здесь также двумерное пространство, но уже с другим расположением объектов… На деле, как видите, это разные вещи.
В первом случае мы сами располагаем нейроны фиксировано в узлах сетки выбранного нами же размера (зависящего от количества нейронов). Во втором же случае это уже совсем другое двумерное пространство, в котором положение определяется значениями признаков каждого из выходных нейронов в отдельности. Проводим обучение, в результате которого снова нейрон-победитель и соседние будут смещаться ближе к подаваемым на вход элементам, что в глобальном итоге приведет к новым значениям весовых коэффициентов. И если мы аналогично отобразим выходные нейроны, то получим:
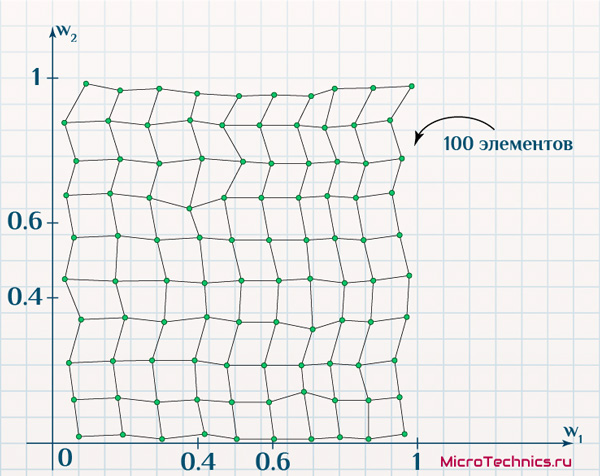
Нейроны смещались в процессе обучения к подаваемым образцам и в итоге повторяют форму, которая соответствует размещению изначальных объектов. В действии еще одно важное свойство самоорганизующихся карт Кохонена – они позволяют «упростить» данные (100 элементов вместо 500), сохраняя взаимозависимости и вид этих данных.
Резюмируем инфографикой со структурой сети и анализом значений признаков до обучения и после:
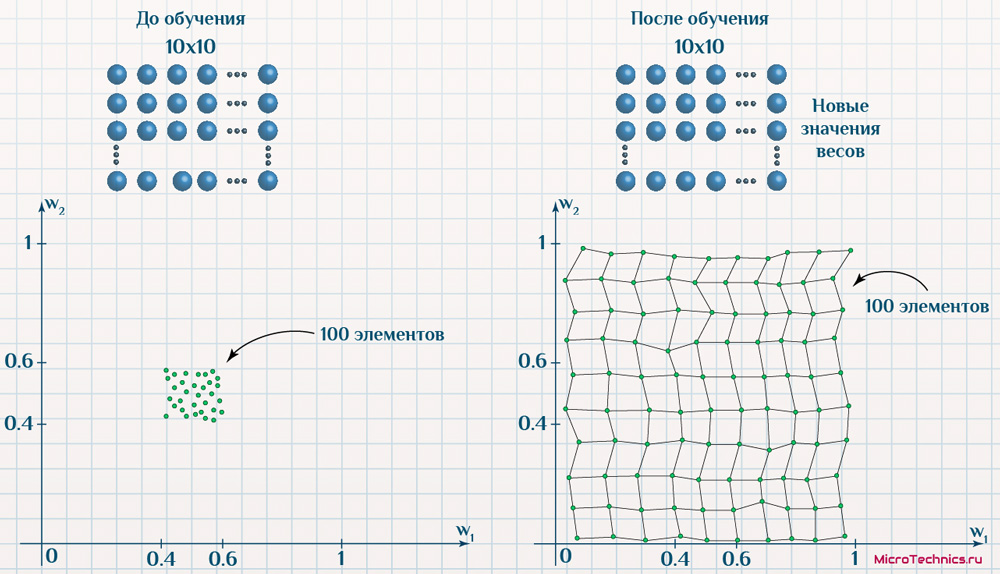
Структура не изменилась, а значения признаков напротив значительно скорректировались.
Пример 4.
Финишируем еще одним примером, похожим на предыдущий, за одним существенным отличием – выходные нейроны располагаются не в двумерном пространстве, а в одномерном. Ключевое отличие будет в механизме определения соседей:
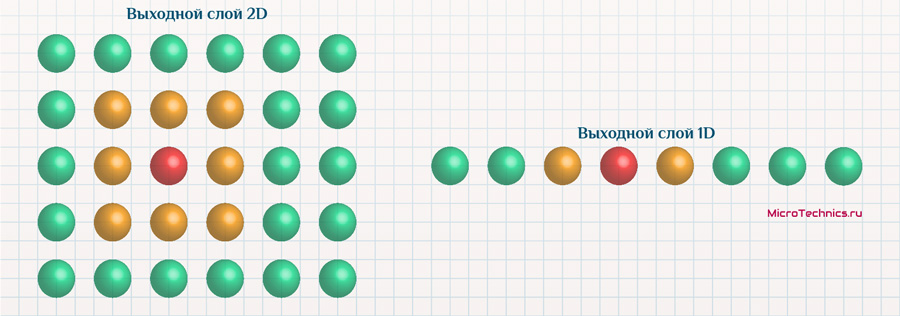
На входе все те же объекты:
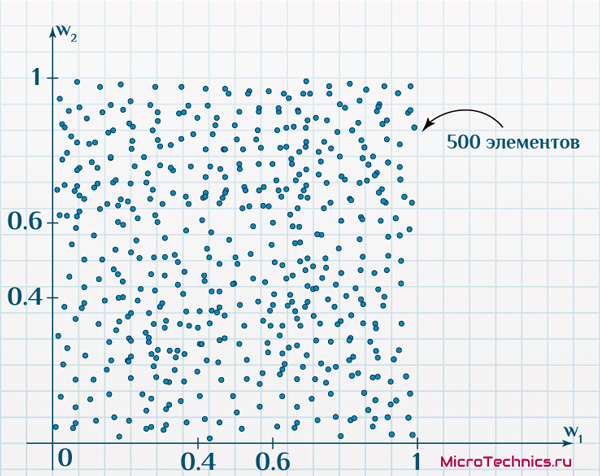
Да и на выходе все те же 100 нейронов, проинициализированные значениями признаков из диапазона (0.4, 0.6). Вот только результат обучения будет другим, что вытекает из изменения размерности пространства:
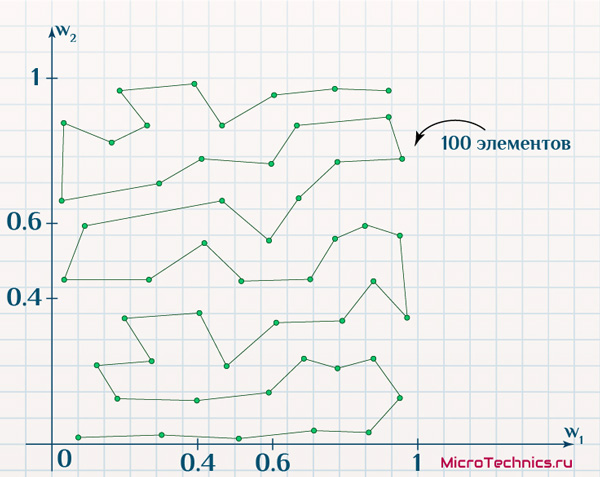
Тем не менее сеть четко работает, то есть значения весовых коэффициентов позволяют выходным нейронам успешно отражать структуру входных данных.
На этом заканчиваем тему нейронных сетей Кохонена, если остались какие-либо вопросы, пишите в комментарии или на наш форум, проблемы решим, вопросы разрешим 🤝