Работа и мощность тока. Переменный и постоянный ток.

Всем доброго времени суток, в сегодняшней статье мы будем разбираться с понятиями работы и мощности электрического тока. Для начала рассмотрим постоянный ток, а затем проведем аналогичные исследования и для цепей переменного тока. Тема довольно обширная, так что стартуем незамедлительно.

Работа и мощность постоянного тока.

Вспомним первую статью курса "Основы электроники" - вот она. Там мы определили напряжение как работу, которую необходимо затратить для переноса единичного заряда из одной точки в другую. Обозначим эту величину - A. Чтобы найти работу, которую совершат несколько зарядов, нам необходимо работу одного заряда умножить на количество зарядов:

A_0 = AN

А мощность по определению - это работа за единицу времени. Таким образом, мы получаем формулу мощности:

P = \frac{A_0}{\Delta t} = \frac{N}{\Delta t}A

Снова возвращаемся к уже упомянутой первой статье курса и в ней мы выяснили, что количество зарядов, проходящее через проводник в единицу времени (\frac{N}{\Delta t}) - это и есть ток по определению. Таким образом, в итоге мы приходим к следующему выражению для мощности электрического тока:

P = IU

Здесь мы также учли, что работа A по перемещению одного заряда численно равна напряжению на данном участке цепи. Собственно, мы получили одну из основных формул для нахождения мощности постоянного тока. А учитывая закон Ома выводим следующее:

P = IU = I(IR) = I^2R

P = IU = \frac{U}{R}\medspace U = \frac{U^2}{R}

Единицей измерения мощности является Ватт, и 1 Вт - это мощность, при которой за 1 секунду совершается работа 1 Джоуль.

Тут необходимо остановиться на одном познавательно-бытовом нюансе. Часто при обсуждении работы электрического тока можно услышать сочетание - киловатт-час. Например, электросчетчики в домах показывают работу именно в этих единицах измерения. Так вот несмотря на схожесть в названиях единиц измерения мощности (ватт) и работы (киловатт - час / ватт - час) не стоит забывать, что эти термины относятся к разным физическим величинам. Чтобы перевести КВт*ч в более привычные с точки зрения системы измерений Си Джоули можно воспользоваться следующим математическим соотношением:

1\medspace КВт\cdotч = 3600000\medspace Дж

Давайте рассмотрим небольшой пример для иллюстрации вышесказанного. Итак, пусть у нас есть чайник, мощность которого составляет 1200 Вт (1.2 КВт). Мысленно включим его на 10 минут (1/6 часа). В итоге, работа электрического тока (а вместе с ней и потребленная чайником энергия) составит:

1200\medspace Вт \cdot 1 / 6\medspace ч = 200\medspace Вт\cdot ч = 0.2\medspace КВт\cdotч

С работой и мощностью постоянного тока все понятно, поэтому перейдем к цепям переменного тока.

Мощность переменного тока.

Пусть у нас ток и напряжение изменяются по следующим законам:

i(t) = I_m\medspace sin(wt\medspace-\medspace \beta)

u(t) = U_m\medspace sin(wt)

Мы приняли, что ток и напряжение сдвинуты по фазе на величину \beta. Мгновенная мощность (мощность переменного тока в любой момент времени) будет равна:

p(t) = u(t)\medspace i(t) = U_m\medspace sin(wt) \cdot I_m\medspace sin(wt\medspace-\medspace \beta)

Преобразуем формулу в соответствии с тригонометрической формулой произведения синусов:

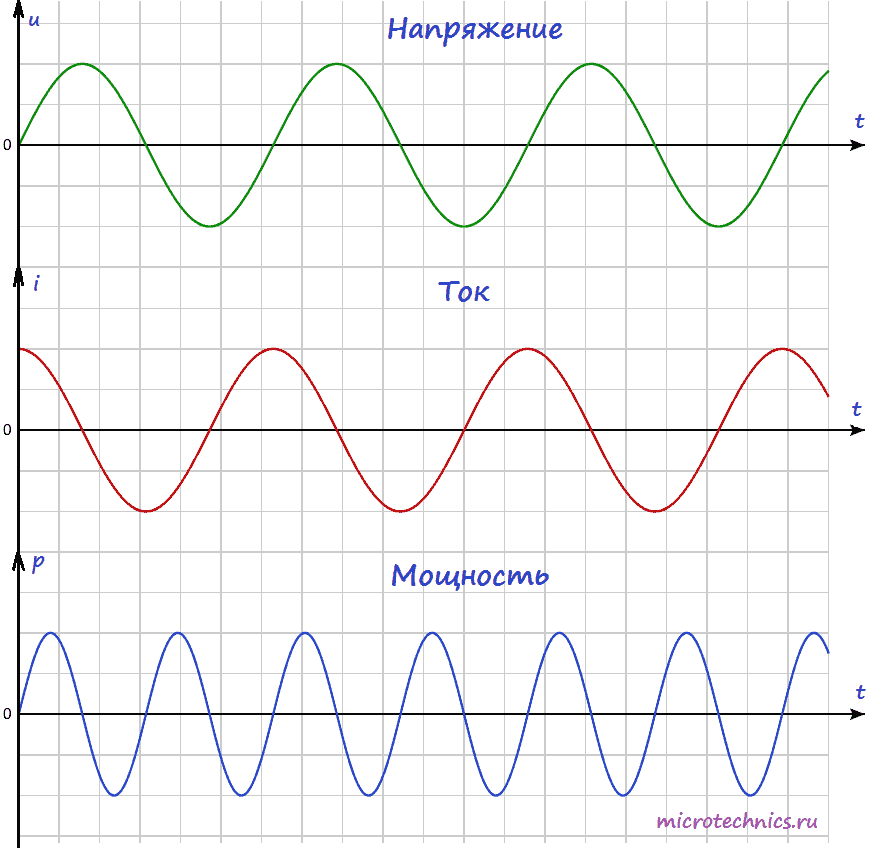
p(t) = U_m\medspace sin(wt)\medspace I_m\medspace sin(wt\medspace-\medspace \beta) = \frac{1}{2}\medspace U_m\medspace I_m\medspace (cos\beta\medspace-\medspace  cos(2wt\medspace-\medspace \beta)) = \\\frac{1}{2}\medspace U_m\medspace I_m\medspace cos\beta\medspace-\medspace \frac{1}{2}\medspace U_m\medspace I_m\medspace cos(2wt\medspace-\medspace \beta)

Вот так будут выглядеть зависимости тока, напряжения и мощности переменного тока от времени:

На самом деле практический интерес представляет не мгновенное значение мощности (которое постоянно меняется), а среднее. Для среднего за период значения записываем:

P =\frac{1}{T}\medspace\int_0^Tp(t)\,\mathrm{d}t

Не буду особо нагружать математическими выкладками, давайте просто обратим внимание на то, что в формуле мгновенной мощности второе слагаемое (-U_m\medspace I_m\medspace cos(2wt\medspace-\medspace \beta)) при интегрировании (суммировании) даст 0. Это связано с тем, что если мы рассматриваем конкретный период, то значение косинуса в течение одного полу-периода сигнала будет иметь положительную величину, а в течение другого - отрицательное. Поэтому в финальной формуле средней мощности переменного тока останется только интеграл от первого слагаемого:

P = \frac{1}{T} \cdot\medspace \frac{1}{2}\medspace I_m\medspace U_m\medspace cos\beta T = \frac{1}{2}\medspace I_m\medspace U_m\medspace cos\beta

По итогу мы получили выражение для вычисления средней за период мощности в цепи переменного тока (ее также называют активной мощностью).

Если сдвиг фаз между током и напряжением будет равен нулю, то значение средней мощности будет максимальным (поскольку cos 0 = 1). В случае сдвига фаз часть мощности передается в нагрузку (активная мощность), а часть нет (реактивная мощность). Реактивная мощность характеризует энергию, которая переходит от источника к реактивным элементам цепи, а затем возвращается этими элементами обратно в источник в течение одного периода. Из формулы понятно, что чем больше cos\beta, тем больше мощности попадет непосредственно в нагрузку, поэтому величину cos\beta называют коэффициентом мощности. Активную мощность мы определили ранее, а вот для реактивной мощности справедлива иная формула:

Q = \frac{1}{2}\medspace I_m\medspace U_m\medspace sin\beta

И тогда полная мощность переменного тока равна:

S = \sqrt{(P^2 + Q^2)}

На сегодня на этом все, мы разобрались с понятиями работы и мощности электрического тока, засим откланиваюсь, до скорого.